Etude de la cinétique de la décomposition de l'eau oxygénée H2O2
Détermination de la concentration de la solution d'eau oxygénée
On dose \(\textrm H_2\textrm O_2\) en utilisant la même réaction que précédemment, mais on opère en présence d'un catalyseur, le molybdate d'ammonium.
Dans ces conditions la réaction est totale et instantanée.
Placer dans l'ordre dans le bécher
\(10 \textrm{cm}^3\) de \(\textrm H_2\textrm O_2\),
\(\frac{1}{2}\) tube à essai de \(\textrm H_2\textrm{SO}_4\) à \(1 \textrm{mol.L}^{-1}\)
\(\frac{1}{2}\) tube à essai de \(\textrm{KI}\) à 10 %
1 tube à essai de solution de molybdate d'ammonium à 1 %.
Remplir la burette avec \(\textrm{Na}_2\textrm S_2\textrm O_3\) de concentration molaire \(\textrm{0,1 mol.L}^{-1}\).
Verser la solution titrée de thiosulfate de sodium dans la solution à doser, en ajoutant de l'empois d'amidon ou du thiodène lorsque la solution est jaune clair.
Poursuivre le dosage jusqu'à ce que la solution devienne incolore.
On utilise \(\textrm{11,2 cm}^3\) de thiosulfate de sodium pour ce dosage.
Traitement des données expérimentales
Calcul la concentration \(C\) de \(\textrm H_2\textrm O_2\) donnée dans le flacon en \(\textrm{mol.L}^{-1}\) :
Equations des réactions du dosage :
\(\mathbf{\textrm H_2\textrm O_2 + 2.(\textrm K^+, \textrm I^-) + (2.\textrm H_3\textrm O^+,\textrm{SO}_4^{2-}) \longrightarrow \textrm I_2 + 4.\textrm H_2\textrm O + (2.\textrm K^+, \textrm{SO}_4^{2-} )}\)
\(\mathbf{2.(\textrm{Na}^+,\textrm S_2\textrm O_3^{2-}) + \textrm I_2\longrightarrow 2.(\textrm{Na}^+, \textrm I^-) + 2.(\textrm{Na}^+,\textrm S_4\textrm O_6^{2-})}\)
A l'équivalence, la quantité d'ions thiosulfate est double de la quantité d'eau oxygénée :
donc \(\mathbf{n(\textrm S_2\textrm O_3^{2-}) = 2 \times n(\textrm H_2\textrm O_2)}\)
d'où \(\mathbf{C(\textrm S_2\textrm O_3^{2-}) \times V(\textrm{Na}_2\textrm S_2\textrm O_3) = 2 \times C ( \textrm H_2\textrm O_2) \times V (\textrm H_2\textrm O_2)}\)
d'où \(\mathbf{C ( \textrm H_2\textrm O_2 ) = \frac{C( \textrm S_2\textrm O_3^{2-}) \times V(\textrm{Na}_2\textrm S_2\textrm O_3)}{2 \times V (\textrm H_2\textrm O_2 )} = \frac{ \textrm{0,1} \times \textrm{11,2}}{2 \times 10} = \textrm{0,056 mol.L}^{-1}}\)
Calcul du nombre de moles de \(\textrm H_2\textrm O_2\) au temps t
Calcul de la quantité d'eau oxygénée \(n_0\) mises dans le bécher au temps \(t = 0\).
On a versé \(10 \textrm{cm}^3\) de \(\textrm H_2\textrm O_2\) à l'aide de la pipette.
Comme la concentration de l'eau oxygénée était de \(\textrm{0,056 mol.L}^{-1}\),
on a donc \(n_0 = \textrm{0,056} \times \textrm{0,001} = \textrm{5,6} \times 10^{-2} \times 1 \times 10^{-3} = \textrm{5,6}.10^{-4}\textrm{ mol}\) dans le bécher.
Calcul de la quantité d'eau oxygénée \(n_t\) restant à doser au temps \(t\) dans le bécher en fonction du volume \(V\) de thiosulfate de sodium versé :
On vient de voir que la quantité d'eau oxygénée réduite par un volume \(V(\textrm{Na}_2\textrm S_2\textrm O_3)\) de thiosulfate de sodium était égale à \(C(\textrm S_2\textrm O_3^{2-}) \times \frac{V (\textrm{Na}_2\textrm S_2\textrm O_3)}{2}\) .
De ce fait, la quantité d'eau oxygénée restant dans le milieu après avoir versé un volume \(V(\textrm{Na}_2\textrm S_2\textrm O_3)\) de thiosulfate de sodium est donc égale à
\(\mathbf{n_t = n_0 - C( \textrm S_2\textrm O_3^{2-}) \times \frac{V (\textrm{Na}_2\textrm S_2\textrm O_3)}{2}}\)
le volume étant exprimé en litre \(V(\textrm{Na}_2\textrm S_2\textrm O_3) = V_\textrm{mL} \times 10^{-3}\)
On a donc
\(\mathbf{n_t = \textrm{5,6} \times 10^{-4} - \textrm{0,100} \times \frac{V_\textrm{mL} \times 10^{-3}}{2} = (\textrm{5,6} - \textrm{0,5} \times V_\textrm{mL}) \times 10^{-4}}\)
Détermination de la constante de vitesse de la réaction de décomposition de l'eau oxygénée
Résultats observés :
V cm3 n | Temps (chronomètre) | Temps moyen (en secondes) | nt = (5,6 - 0,5 x VmL) x 10-4 |
|---|---|---|---|
1 | 00:50 | 50 | 5,1 x 10-4 |
2 | 01:53 | 113 | 4,6 x 10-4 |
3 | 02:55 | 175 | 4,1 x 10-4 |
4 | 04:09 | 249 | 3,6 x 10-4 |
5 | 05:34 | 334 | 3,1 x 10-4 |
6 | 07:01 | 421 | 2,6 x 10-4 |
7 | 09:03 | 543 | 2,1 x 10-4 |
8 | 11:17 | 677 | 1,6 x 10-4 |
9 | 14:24 | 864 | 1,1 x 10-4 |
Hypothèse de réaction au premier ordre :
\(\mathbf{\textrm H_2\textrm O_2 + 2.\textrm I^- + 2.\textrm H_3\textrm O^+ \longrightarrow 4.\textrm H_2\textrm O + \textrm I_2}\)
Si la réaction de décomposition de l'eau oxygénée est du premier ordre par rapport à l'eau oxygénée, alors la vitesse de réaction s'exprimera par la relation :
\(\mathbf{\textrm v = \frac{\textrm d(C_{\textrm H_2\textrm O_2})}{\textrm dt} = k' (C_{\textrm H_2\textrm O_2})}\)
soit \(\mathbf{\ln (C_{t,\textrm H_2\textrm O_2}) = k' \times t + \textrm{cte}}\)
comme pour\( t = 0\), la concentration initiale est \(C_{0,\textrm H_2\textrm O_2}\), on a \(cte = \ln(C_{0,\textrm H_2\textrm O_2})\)
d'où \(\mathbf{\ln (C_{t,\textrm H_2\textrm O_2}) = k' \times t + \ln (C_{0,\textrm H_2\textrm O_2})}\)
et \(\mathbf{\ln\frac{C_{t,\textrm H_2\textrm O_2}}{C_{0,\textrm H_2\textrm O_2}}=f(t)}\)
d'où le tableau complété :
V cm3 n | Temps (chronomètre) | Temps moyen (en secondes) | nt = (5,6 - 0,5 x VmL) x 10-4 | \(ln \frac{C_{t,H_2O_2}}{C_{0,H_2O_2}}=f(t)\) |
|---|---|---|---|---|
1 | 00:50 | 50 | 5,1 x 10-4 | 0,094 |
2 | 01:53 | 113 | 4,6 x 10-4 | 0,197 |
3 | 02:55 | 175 | 4,1 x 10-4 | 0,312 |
4 | 04:09 | 249 | 3,6 x 10-4 | 0,442 |
5 | 05:34 | 334 | 3,1 x 10-4 | 0,591 |
6 | 07:01 | 421 | 2,6 x 10-4 | 0,767 |
7 | 09:03 | 543 | 2,1 x 10-4 | 0,981 |
8 | 11:17 | 677 | 1,6 x 10-4 | 1,253 |
9 | 14:24 | 864 | 1,1 x 10-4 | 1,627 |
Traçons les points représentatifs de cette variation \(\mathbf{\ln\frac{C_{t,\textrm H_2\textrm O_2}}{C_{0,\textrm H_2\textrm O_2}}=f(t)}\)
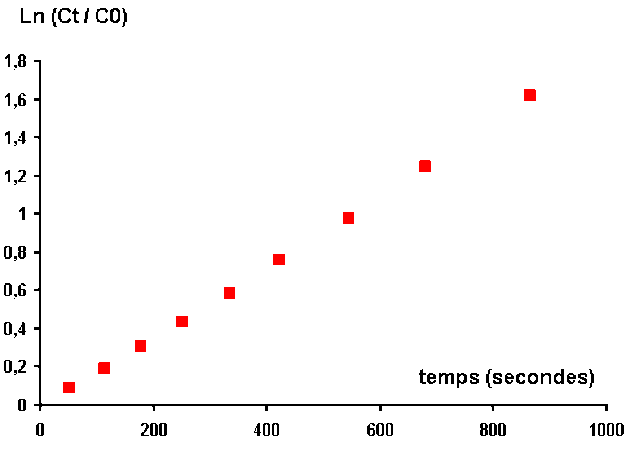
On observe que tous les points sont alignés.
L'hypothèse de réaction au premier ordre est donc vérifié.
On peut relier ces points et faire le calcul du coefficient directeur de la droite. On obtient :
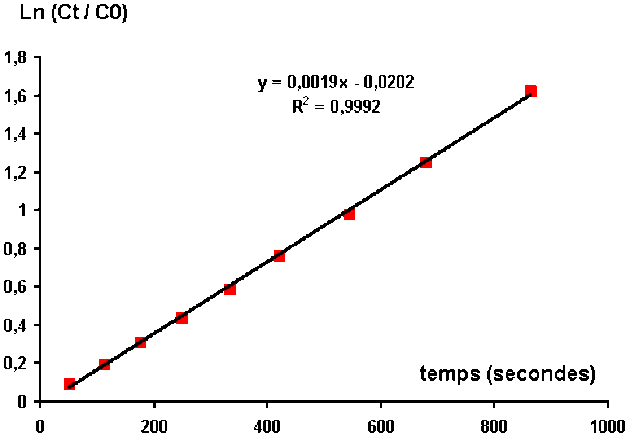
Le coefficient de vitesse de la réaction est donc de 0,0019 s-1.