La densité de probabilité de présence
La fonction d'onde est une amplitude de probabilité de présence et le carré de sa norme représente la densité volumique de probabilité de présence de la particule.
\(\mathbf{\mid\Psi\mid^2=\frac{\textrm dP}{\textrm dV}}\)
C'est une propriété ponctuelle. En chaque point de l'espace, on peut calculer cette densité volumique à partir de l'expression de la fonction d'onde.
\(\mathrm{dV}\) peut être associé à un élément de volume infinitésimal. La probabilité de présence élémentaire \(\mathrm{dP}\) de la particule à l'intérieur de ce volume \(\mathrm{dV}\) est :
\(\mathbf{\textrm dP=\mid\Psi\mid^2\textrm dV}\)
Si on veut calculer la probabilité de présence de la particule \(\mathrm{P(V)}\) à l'intérieur d'un volume fini, il faut procéder à une intégration sur ce volume de la probabilité élémentaire :
\(\mathbf{P(V)=\displaystyle{\int_V}\mid\Psi\mid^2.\textrm dV}\)
Dans le système de coordonnées cartésiennes par exemple, cette intégration revient à une intégrale triple sur \(\textrm x\), \(\textrm y\) et \(\textrm z\) mais on a souvent intérêt à faire des changements de coordonnées adaptés au type de volume d'intégration.
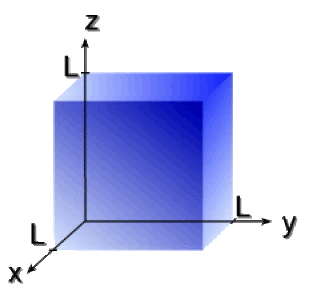
Exemple : Un cube
Dans un cube d'arête \(\textrm L\) tel que représenté ci-contre, on conserve les coordonnées cartésiennes \(\textrm x\), \(\textrm y\) et \(\textrm z\). Le volume élémentaire est alors :
\(\mathrm{dV= dx. dy. dz}\)
Il vient alors :
\(\mathbf{P(V)=\displaystyle{\int\int}\displaystyle{\int^L_{x,y,z=0}}\mid\Psi\mid^2.\textrm dx.\textrm dy.\textrm dz}\)
Exemple : Une sphère
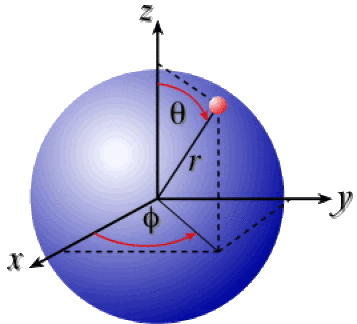
Dans une sphère de rayon \(\textrm R\), on utilisera les coordonnées sphériques \(\textrm r\), \(\theta\) et \(\varphi\). Le volume élémentaire est alors :
\(\mathrm{dV=r^2.\sin\theta. dr. d\theta.\textrm d\varphi}\)
Il vient alors :
\(\mathbf{P(V)=\displaystyle{\int^\textrm R_{r=0}\int^\pi_{\theta=0}\int^{2.\pi}_{\varphi=0}}\mid\Psi\mid^2.r^2.\sin\theta.\textrm dr.\textrm d\theta.\textrm d\varphi}\)