Formules d'addition et de multiplication par 2
Quels que soient les réels \(a\) et \(b\) :
\(\boxed{\cos{(a+b)} = \cos{a}\cos{b} - \sin{a}\sin{b}}\)
\(\boxed{\cos{(a-b)} = \cos{a}\cos{b} + \sin{a}\sin{b}}\)\(\)
\(\boxed{\sin{(a+b)} = \sin{a}\cos{b} + \cos{a}\sin{b}}\)\(\)
\(\boxed{\sin{(a - b)} = \sin{a}\cos{b} - \cos{a}\sin{b}}\)\(\)
Explication : à support géométrique
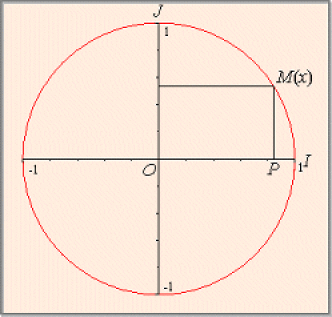
Soit le cercle \(C\) muni du point origine \(I\) et soit \((O, \overrightarrow{i}, \overrightarrow{j})\)le repère orthonormé direct tel que \(\overrightarrow{i} = \overrightarrow{OI}.\)
La surjection \(\rho\) de \(R\) sur le cercle \(C\) définie dans l'introduction dépend du point origine \(I\) choisi sur \(C.\) Soit \(x\) un réel et \(M\) son image sur \(C.\)
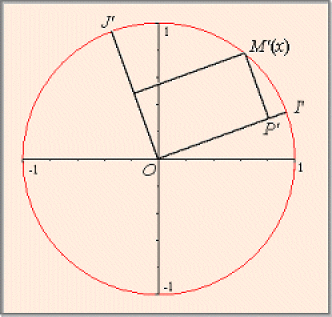
Si \(C\) est muni d'un autre point origine \(I',\) la surjection \(\rho'\)correspondante associe à ce réel \(x\) un autre point sur \(C.\) On admet que les réels \(\cos{x}\) et\(\sin{x}\) ne dépendent pas du point origine choisi sur \(C.\)
\(\cos{x} = \overrightarrow{OI}.\overrightarrow{OM}\)
\(\cos{x} = \overrightarrow{OI'}.\overrightarrow{OM'}\)
Soit \(a\) et \(b\) deux réels et \(A\) et \(B\) leurs images sur le cercle \(C\) muni du point origine \(I.\) Dans le repère orthonormé \((O,\overrightarrow{i}, \overrightarrow{j})\) \(A\) a pour couple de coordonnées \((\cos{a}, \sin{a})\)et \(B\) a pour couple de coordonnées \((\cos{b}, \sin{b}).\)
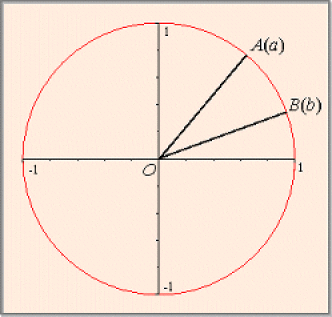
On a donc \(\overrightarrow{OA}.\overrightarrow{OB} = \cos{a}\cos{b} + \sin{a}\sin{b}\)
On admet que si le cercle \(C\) est muni du point origine \(B\) alors le point \(A\) est l'image du réel \(a - b.\)
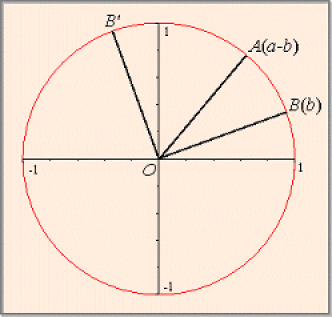
\(\overrightarrow{OA}.\overrightarrow{OB} = \cos{(a-b)}\)
D'où \(\cos{(a-b)} = \cos{a}\cos{b} + \sin{a}\sin{b}.\)
La formule donnant \(\cos{(a+b)}\)s'obtient en remplaçant \(b\) par\(-b\) dans la formule donnant \(\cos{(a-b)}.\)
En appliquant la formule donnant \(\cos{(a-b)}\)
on a \(\cos{(\frac{\pi}{2} - x)} = \cos{\frac{\pi}{2}}\cos{x} + \sin{\frac{\pi}{2}}\sin{x} = \sin{x}\)et donc\(\sin{(\frac{\pi}{2}-x)} = \cos{x}\) d'où \(\sin{(a+b)}=\cos{(\frac{\pi}{2}-a-b)} = \cos{(\frac{\pi}{2}-a)}\cos{b}+\sin{(\frac{\pi}{2}-a)}\sin{b}\) \(=\sin{a}\cos{b}+\cos{a}\sin{b}\)
La formule donnant \(\sin{(a-b)}\)s'obtient en remplaçant \(b\) par\(-b\) dans la formule donnant \(\sin{(a+b)}.\)
Explication : à l'aide des nombres complexes
Soit \(C\) le cercle de centre \(O\) et de rayon \(1,\) orienté dans le sens direct et muni d'un point origine \(I\) et soit \((O,\overrightarrow{i},\overrightarrow{j})\)le repère orthonormé direct tel que \(\overrightarrow{i} = \overrightarrow{OI}.\)
Soit \(M\) l'image du réel \(x.\)
Dans le repère \((O,\overrightarrow{i},\overrightarrow{j})\) le point \(M\) a pour coordonnées \((\cos{x}, \sin{x}).\)
L'application \(\theta\) qui, à tout point \(N\) du cercle \(C\) de coordonnées \((a, b),\) associe le nombre complexe \(z=a+ib\) est une bijection du cercle \(C\) sur l'ensemble \(U\) des nombres complexes de module \(1.\) On considère l'application \(\theta \circ \rho\):
\(R \xrightarrow{\rho}C\xrightarrow{\theta}U\)
\(x \mapsto M \mapsto z\)
L'application \(\theta \circ \rho,\) notée \(\Phi,\) est une surjection de \(\mathbb R\) sur \(U.\) Soit \(x\) un réel quelconque. L'image de ce réel \(x\) par\(\Phi\) est le nombre complexe \(z\) tel que \(z = \cos{x} + i\sin{x}.\)
On admet que l'application \(\Phi\)transforme la somme en produit, c'est-à-dire vérifie la propriété suivante : \(\forall (x, x') \in \mathbb R ^2~~\Phi(x+x') = \Phi(x).\Phi(x').\)
Cette propriété a pour conséquence l'égalité suivante :
\(\cos{(x+x')} + i\sin{(x+x')} = (\cos{x} + i\sin{x})(\cos{x'} + i\sin{x'})\)
d'où \(\cos{(x+x')} = \cos{x}\cos{x'} -\sin{x}\sin{x'}\) et \(\sin{(x+x')} = \sin{x}\cos{x'} + \cos{x}\sin{x'}\)
Remarque :
Cette application \(\Phi\)est aussi notée \(x \mapsto e^{ix}.\) Cette notation exponentielle donne un formalisme très utile dans les calculs.
Les formules donnant \(\cos{(a-b)}\)et \(\sin{(a-b)}\)s'obtiennent en remplaçant \(b\) par \(-b\)dans les formules donnant \(\cos{(a+b)}\) et \(\sin{(a+b)}.\)
Quels que soient les réels \(a\) et \(b\) tels que \(a,~b~\textrm{et}~a+b\) et n'appartiennent pas à l'ensemble \(\{\frac{\pi}{2}+k\pi, k \in \mathbb Z\}\):
\(\boxed{\tan{(a+b)} = \frac{\tan{a} + \tan{b}}{1-\tan{a}\tan{b}}}\)
\(\boxed{\tan{(a-b)} = \frac{\tan{a}-\tan{b}}{1+\tan{a}\tan{b}}}\)
Explication :
Soient des réels \(a\) et \(b\) tels que \(a,~b~\textrm{et}~a+b\) et n'appartiennent pas à l'ensemble \(\{\frac{\pi}{2}+k\pi, k \in \mathbb Z\}\)
\(\tan{(a+b)} = \frac{\sin{(a+b)}}{\cos{(a+b)}} = \frac{\sin{a}\cos{b}+\cos{a}\sin{b}}{\cos{a}\cos{b}-\sin{a}\sin{b}}\)
en divisant le numérateur et le dénominateur par le produit non nul \(\cos{a}\cos{b}\)
\(\tan{(a+b)} = \frac{\frac{\sin{a}\cos{b}}{\cos{a}\cos{b}}+\frac{\cos{a}\sin{b}}{\cos{a}\cos{b}}}{\frac{\cos{a}\cos{b}}{\cos{a}\cos{b}}-\frac{\sin{a}\sin{b}}{\cos{a}\cos{b}}} = \frac{\tan{a}+\tan{b}}{1-\tan{a}\tan{b}}\)
La deuxième formule est obtenue en remplaçant \(b\)par \(-b\)dans l'égalité précédente.
Pour tout réel \(a\) :
\(\boxed{\cos{2a} = \cos^2{a} - \sin^2{a} = 2\cos^2{a} - 1 = 1 - 2\sin^2{a}}\)
\(\boxed{\sin{2a} = 2\sin{a}\cos{a}}\)
Pour tout réel \(a\) n'appartenant pas à l'ensemble \(\{\frac{\pi}{2}+k\pi, k \in \mathbb Z\}~~\bigcup~~\{\frac{\pi}{4}+k\frac{\pi}{2}, k \in \mathbb Z \}\):
\(\boxed{\tan{2a} = \frac{2\tan{a}}{1 - \tan^2{a}}}\)
Explication :
Il suffit de remplacer \(b\) par \(a\) dans les formules précédentes donnant \(\cos{(a+b)},\) \(\sin{(a+b)}\) et \(\tan{(a+b)}.\)
Pour tout réel \(a\):
\(\boxed{\cos^2{a} = \frac{1+\cos{2a}}{2}~~~~\sin^2{a} = \frac{1-\cos{2a}}{2}}\)
Explication :
Ces formules sont obtenues à partir de la formule \(\cos{2a} = 2\cos^2{a} - 1 = 1 - 2\sin^2{a}.\)
Pour tout réel \(x\) n'appartenant pas à l'ensemble \(\{\pi +2k\pi, k \in \mathbb Z \}\):
\(\boxed{\textrm{Si on pose}~~t = \tan{\frac{x}{2}},~~\cos{x} = \frac{1 -t^2}{1+t^2}~~~~~~\sin{x}=\frac{2t}{1+t^2}}\)
Pour tout réel \(x\) n'appartenant pas à l'ensemble \(\{\pi +2k\pi, k \in \mathbb Z \}~~\bigcup~~\{\frac{\pi}{2}+k\pi, k \in \mathbb Z \}\)
\(\boxed{\textrm{Si on pose} ~~t = \tan{\frac{x}{2}},~~\tan{x} = \frac{2t}{1-t^2}}\)
Explication :
Soit \(x \neq \pi + 2k\pi,\) \(k\in \mathbb Z .\)
\(\cos{x} = \cos^2{\frac{x}{2}} - \sin^2{\frac{x}{2}} = \frac{\cos^2{\frac{x}{2}} - \sin^2\frac{x}{2}}{\cos^2\frac{x}{2}+\sin^2\frac{x}{2}}\)
Puis on divise le numérateur et le dénominateur par \(\cos^2\frac{x}{2}\)qui est non nul car \(x \neq \pi + 2k\pi,\) \(k\in \mathbb Z .\)
\(\sin x = 2\sin \frac{x}{2}\cos\frac{x}{2} = \frac{2\sin\frac{x}{2}\cos\frac{x}{2}}{\sin^2\frac{x}{2}+\cos^2\frac{x}{2}}\)
Puis on divise le numérateur et le dénominateur par \(\cos^2\frac{x}{2}.\)