Fonctions usuelles et leurs réciproques

Soit \(\mathbb F(]-\alpha, +\alpha[,\mathbb R)\)l'espace vectoriel des fonctions numériques définies sur l'intervalle \(]-\alpha, +\alpha[.\) Alors \(\mathbb F(]-\alpha, +\alpha[,\mathbb R) = \mathbb P \oplus \mathbb I\)où \(\mathbb P\)désigne l'espace vectoriel des fonctions paires réelles et \(\mathbb I\)celui des fonctions impaires réelles.

Cela s'énonce plus précisément de la façon suivante : Toute fonction numérique définie sur un intervalle \(]-\alpha, +\alpha[\)peut s'écrire de manière unique comme la somme d'une fonction paire et d'une fonction impaire.

\(\forall f \in \mathbb F(]-\alpha, +\alpha[,\mathbb R)~~~\exists(p,i) \in \mathbb P \times \mathbb I~~f = p+i\)

\(\forall x \in ]-\alpha, +\alpha[~~p(x) = \frac{f(x) + f(-x)}{2}~~i(x) = \frac{f(x)-f(-x)}{2}.\)

La fonction \(p\) est appelée partie paire de \(f\) et la fonction \(i\) sa partie impaire.

On appelle cosinus hyperbolique et sinus hyperbolique la partie paire et la partie impaire de la fonction exponentielle

\(\boxed{\forall x\in\mathbb R~~\textrm{ch} x = \frac{e^x+e^{-x}}{2}}\boxed{\forall x \in \mathbb R~~\textrm{sh}x = \frac{e^x-e^{-x}}{2}}\)

\(\boxed{\forall x \in \mathbb R}\\\boxed{\textrm{ch}x+\textrm{sh}x=e^x}\boxed{\textrm{ch}x-\textrm{sh}x=e^{-x}}\boxed{\textrm{ch}^2x-\textrm{sh}^2x=1}\)

Les fonctions ch et sh sont continues et dérivables sur \(\mathbb R.\) En appliquant les opérations sur les fonctions dérivables il vient :

\(\boxed{\forall x \in \mathbb R,~~(\textrm{ch})'(x)=\textrm{sh}x,~~(\textrm{sh})'(x) = \textrm{ch}x}\)

\(\forall x \in \mathbb R~~\textrm{ch}x>0 \Rightarrow (\textrm{sh})'(x) > 0\)donc la fonction sh est strictement croissante,

de plus\(\displaystyle \lim_{x \rightarrow +\infty}\textrm{sh}x=+\infty\) et en utilisant l'imparité \(\displaystyle \lim_{x\rightarrow-\infty}\textrm{sh}x=-\infty,\) enfin \(\textrm{sh}0=0.\)

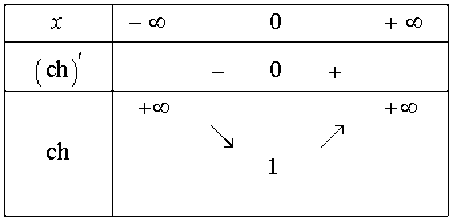
Alors \(\forall x <0~~\textrm{sh}x<0,~~\forall x>0~~\textrm{sh}x>0\)donc la fonction ch est strictement décroissante sur \(]-\infty, 0]\)et strictement croissante sur \([0,+\infty[,\) de plus \(\displaystyle \lim_{x\rightarrow+\infty}\textrm{ch}x=+\infty\)et en utilisant la parité \(\displaystyle \lim_{x\rightarrow-\infty}\textrm{ch}x=+\infty,\) enfin \(\textrm{ch}0 = 1.\)

Les tableaux de variations suivants résument les propriétés de ces fonctions :

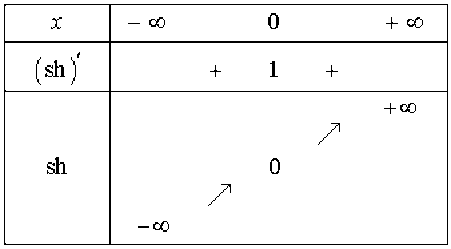
\(\color{red} x \mapsto \textrm{ch}x\)

\(\color{blue} x \mapsto \textrm{sh}x\)

\(\color{green}x \mapsto \frac{1}{2}e^x\)

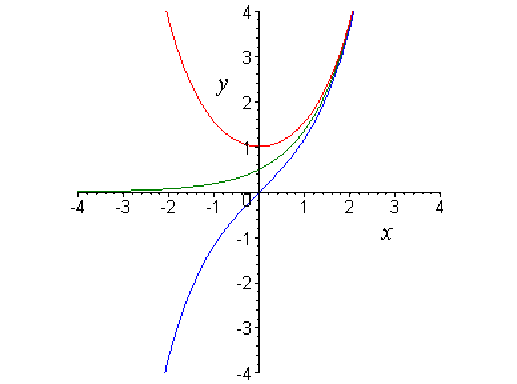
Par lecture des graphes, on retrouve que le graphe de sh est symétrique par rapport à l'origine, celui de ch par rapport à l'axe des \(y.\)

Les deux graphes présentent des branches paraboliques de direction verticale car \(\displaystyle \lim_{x\rightarrow+\infty}\frac{\textrm{sh}x}{x} = \displaystyle \lim_{x\rightarrow+\infty}\frac{\textrm{ch}x}{x}=+\infty\)puis on utilise les symétries.

Au voisinage de \(+\infty\)les deux graphes sont asymptotes au graphe de \(\frac{1}{2}\exp,\) en effet \(\textrm{sh}x<\frac{1}{2}e^x<\textrm{ch}x,\) \(\displaystyle \lim_{x\rightarrow+\infty}(\textrm{ch}x-\textrm{sh}x) = \displaystyle \lim_{x\rightarrow+\infty}e^{-x}=0.\)