Exercice n°1
Partie
Question
Soient \(f\) et \(g\) les fonctions rationnelles définies par
\(\displaystyle{f(x)=\frac{x^2-2x+1}{7x^2+3x+1}}\) et \(\displaystyle{g(x)=\frac{-x^4+1}{x^3+5x+1}}\)
Etudier les graphes de \(f\) et \(g\) au voisinage de \(0\), (tangente, position par rapport à la tangente).
Rappel de cours
Voici la définition des développements limités.
Soit \(f\) définie sur un voisinage pointé de \(0\), noté \(V^*(0)\). On dit que \(f\) possède un développement limité à l'ordre \(n\) en \(0\), si
il existe un polynôme \(P_n(x)\) de degré inférieur ou égal à \(n\) ;
il existe une fonction \(\epsilon\) définie sur \(V^*(0)\), vérifiant \(\displaystyle{\lim_{x\rightarrow0}\epsilon(x)=0}\), tels que :
\(f(x)=P_n(x)+x^n\epsilon(x)\) ;
\(P_n\) est appelé partie principale, et \(x^n\epsilon(x)\) reste, du développement limité.
Comment peut-on reconnaître l'ordre d'un développement limité donné ? Ce n'est pas en regardant le degré du polynôme, car la connaissance de \(p\le n\) ne permet pas de connaître \(n\)... C'est en regardant l'exposant de \(x\) dans le reste \(x^n\epsilon(x)\) ; et c'est pour cela que l'écriture correcte du reste est essentielle.
Par exemple \(2+3x-7x^3+x^5\epsilon(x)\) (il est sous-entendu que \(\displaystyle{\lim_{x\rightarrow0}\epsilon(x)=0}\)) est un développement limité à l'ordre \(5\) (et non pas à l'ordre \(3\)).
Solution détaillée
Pour connaitre la tangente aux courbes, on développe à l'ordre \(1\).
Les deux fonctions ont le même développement limité à l’ordre \(1\) et donc la même tangente
\(f(x)=1-5x+x\epsilon_1(x) \quad g(x)=1-5x+x\epsilon_2(x)\)
Pour connaitre la position relative des deux courbes et de leur tangente, on développe à l'ordre \(2\)
\(f(x)=1-5x+9x^2+x^2\epsilon_1(x)=P_2(x)+x^2\epsilon(x)\)
\(g(x)=1-5x+25x^2+x^2\epsilon_2(x)=Q_2(x)+x^2\epsilon(x)\)
Les deux courbes sont au-dessus de leur tangente, \(g\) est au-dessus de \(f\).
Observation :
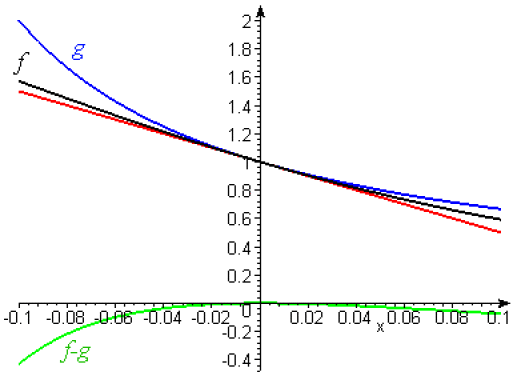
On trace les deux fonctions, \(f\) en noir et \(g\) en bleu.
Les développements de \(f\) et \(g\) à l’ordre \(1\) sont les mêmes :
\(f(x)=1-5x+x\epsilon_1(x)\quad g(x)=1-5x+x\epsilon_2(x)\)
les deux fonctions ont le même développement limité à l’ordre \(1\) et donc la même tangente. Sur un même graphique, on trace \(f\) en noir, \(g\) en bleu et la tangente commune en rouge ainsi que la différence \(f-g\).
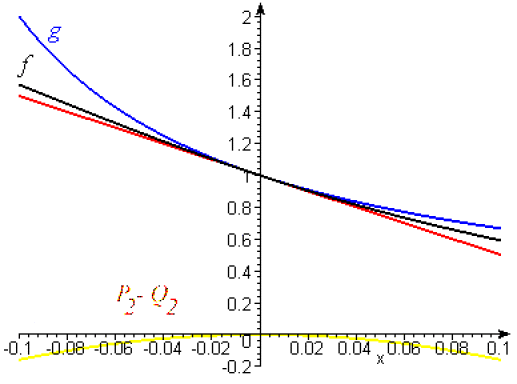
On cherche les développements au deuxième ordre
\(f(x)=1-5x+9x^2+x^2\epsilon_1(x)\)
\(g(x)=1-5x+25x^2+x^2\epsilon_2(x)\)
Sur un même graphique, on trace \(f\) en noir, \(g\) en bleu et la tangente commune en rouge ainsi que la différence \(P_2-Q_2\).
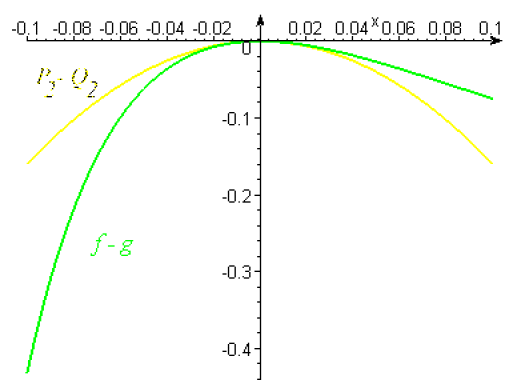
Comparons les ordres de grandeurs de \(f-g\) et de \(P_2-Q_2\)