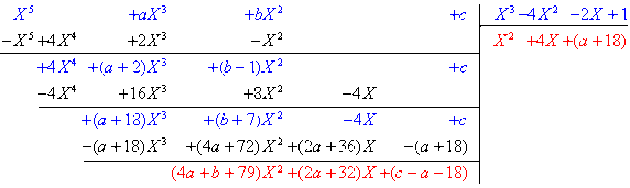Recherche de divisibilité
Partie
Question
Soit les polynômes
\(A(X)=X^3-4X^2-2X+1\), \(B(X)=X^5+aX^3+bX^2+c (a,b,c\in R)\)
Existe-t-il des réels \(a, b, c\) tels que le polynôme \(B(X)\)soit divisible par \(A(X)\)dans \(R[X]\)?
Répondre à cette question par deux méthodes :
En effectuant la division euclidienne de \(B\) par \(A\).
En introduisant un polynôme \(C\) tel que \(B=AC\).
Aide simple
Un polynôme est nul si et seulement si tous ses coefficients sont nuls.
Deux polynômes, non nuls, sont égaux si et seulement si ils ont le même degré et leurs coefficients de mêmes indices sont égaux.
Aide méthodologique
Traduire la divisibilité de \(B\) par \(A\) par : 'le reste de la division euclidienne de \(B\) par \(A\) est nul'.
Rechercher \(C\) de la forme \(C(X)=X^2+^\alpha X+\beta\) et effectuer le produit des polynômes \(A\) et \(C\).
Aide à la lecture
Le but de l'exercice est de rechercher des réels \(a, b, c\) rendant le polynôme \(B\) divisible par le polynôme \(A\).
Solution détaillée
En effectuant la division euclidienne de \(B\) par \(A\) on obtient :
Le dernier reste calculé est soit nul soit de degré au plus 2 donc strictement inférieur au degré de \(A\), alors on arrête là.
L'identité de la division euclidienne s'écrit \(B=AQ+R\)
avec \(Q(X)=X^2+4X+(a+18)\) et \(R(X)=(4a+b+79)X^2+(2a+32)X+(c-a-18)\).
La divisibilité de \(B\) par \(A\) est équivalente à donc à la nullité des trois coefficients de \(R\). Cela conduit au système :
\(\left\{\begin{array}{ccc}4a+b&=&-79\\2a&=&-32\\-a+c&=&18\end{array}\right.\)
système qui a une unique solution \(a=-16\), \(b=-15\), \(c=2\).
Conclusion : il existe des réels \(a, b, c,\) tels que le polynôme \(B(X)\) soit divisible par \(A(X)\), dans ce cas \(B(X)=X^5-16X^3-15X^2+2\).
On recherche un polynôme \(C\) tel que \(B=AC\).
\(B\) et \(A\) étant unitaires, de degrés respectifs 5 et 3, il est naturel de chercher \(C\) unitaire de degré 2 donc de la forme \(C(X)=X^2+\alpha X+\beta\) \((\alpha,\beta\in R)\). Alors :
\(\begin{array}{ccc}A(X)C(X)&=&(X^3-4X^2-2X+1)(X^2+\alpha X+\beta)\\&=&X^5+(\alpha-4)X^4+(\beta-4\alpha-2)X^3+(-4\beta-2\alpha+1)X^2+(\alpha-2\beta)X+\beta\end{array}\)
Donc \(B\) est divisible par \(A\) si et seulement le système suivant a des solutions :
\(\left\{\begin{array}{ccc}\alpha-4&=&0\\-4\alpha+\beta-2&=&a\\-2\alpha-4\beta+1&=&b\\\alpha-2\beta&=&0\\\beta&=&c\end{array}\right.\) \(\Leftrightarrow\) \(\left\{\begin{array}{ccc}\alpha&=&4\\\beta&=&a+18\\-4\beta&=&b+7\\-2\beta&=&-4\\\beta&=&c\end{array}\right.\) \(\Leftrightarrow\) \(\left\{\begin{array}{ccc}\alpha&=&4\\\beta&=&2\\-4\beta&=&b+7\\\beta&=&a+18\\\beta&=&c\end{array}\right.\)
Ce dernier système n'a de solutions que si \(c=2\),\(a+18=2\),\(b+7=-8\).
D'où l'existence et l'unicité des réels cherchés \(a=-16\),\(b=-15\),\(c=2\).
On retrouve ainsi \(B(X)=X^5-16X^3-15X^2+2\).