Spectrographe à réseau
Partie
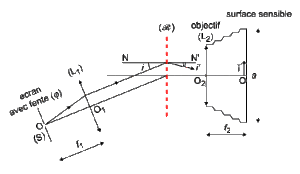
Un spectrographe à réseau est composé :
d'un collimateur dont la lentille (\(L_1\)) est supposée parfaitement achromatique,
d'un réseau par transmission \(R\) comportant \(n\) traits par mètre (son pas\(p\)est donc égal à \(1/n)\)
d'un appareil photographique dont l'objectif, supposé parfaitement achromatique, est assimilable à une lentille (\(L_2\)) de distance focale \(f_2\). La mise au point est effectuée sur l'infini. L'axe optique de (\(L_2\)) est perpendiculaire au plan du réseau en son milieu. La surface sensible est un carré de centre \(O\) et de côté \(a\) ; elle est munie du repère \((O, \vec i)\), le vecteur \(\vec i\) étant vertical ascendant.
La fente d'entrée (\(\varphi\)) du collimateur et les traits du réseau sont horizontaux et perpendiculaires au plan de la figure.
On appelle respectivement \(i\) et \(i'\) les angles d'incidence et d'émergence des rayons lumineux qui traversent le réseau \(R\). Par convention, les angles \(i\) et \(i'\) sont de même signe si les rayons incidents et émergents sont situés d'un même coté de la normale \(N'N\) au plan du réseau.
Question
Quel phénomène physique a lieu au niveau de chaque fente du réseau ? En faire une brève description qualitative. De quels paramètres dépend-il ?
Solution détaillée
les fentes du réseau étant extrêmement fines, chacune se comporte comme une source émettant dans toutes les directions. Il y a alors phénomène de diffraction ; il dépend de la largeur des fentes et de la longueur d'onde utilisée.
Question
La source de lumière \((S)\) émet une lumière monochromatique de longueur d'onde \(\lambda_0\) dans le vide et la fente \((\varphi)\) est supposée infiniment fine. L'angle d'incidence \(i\) étant fixé, à quelle condition les rayons qui émergent du réseau avec l'angle \(i'\) donnent-ils un maximum de lumière sur la surface sensible ? (la réponse devra être brièvement justifiée)
Solution détaillée
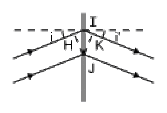
La lumière arrive sur le réseau avec un angle \(i\). Considérons celle qui en sort avec l'angle \(i'\). Regardons ce qui se passe entre deux fentes successives distantes de \(p = \frac{1}{n}\).
Les deux rayons incidents ont même trajet jusqu'au front \(HJ\). Les deux rayons émergents ont même trajet à partir du front \(KJ\). La différence de marche est donc \(HI + IK = p (\sin i + \sin i')\) si l'on compte les deux angles positivement. Il y a un maximum de lumière dans la direction \(i'\) si cette différence de marche correspond à un nombre entier de longueur d'onde donc si
\(\sin i' = k . n . \lambda_0 - \sin i\)
Il faudrait même écrire \(i_k'\)
Question
Le spectrographe précédent étant utilisé en incidence normale \((i=0)\), exprimer en fonction de \(n\), \(\lambda_0\), \(f_2\) et \(a\) le nombre de raies lumineuses, supposées infiniment fines, qui se forment sur la surface sensible de l'appareil photographique.
Préciser leur abscisse \(x\) dans le repère \((O, \vec i)\).
Application numérique :
\(n = 2,80 . 10^5\) traits par mètre ;
\(\lambda_0 = 589,3 ~ \mathrm{nm}\) (raie D du sodium) ;
\(f_2 = 80 ~ \mathrm{mm}\) ;
\(a = 6 ~ \mathrm{cm}\).
Solution détaillée
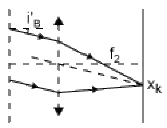
En incidence normale \(\sin i_k' = k.n.\lambda_0\). Les abscisses \(x_k\) des raies lumineuses sur la pellicule sont données par
\(x_k = f_2 ~ \tan i_k' = f_2 \frac{k.n.\lambda_0}{\sqrt{1 - k^2 n^2 \lambda_0^2}}\)
Avec les données, on calcule que \(x_0 = 0\) (raie centrale), \(x_1 = \pm 1,34 ~ \mathrm{cm}\) et
\(x_3 = \pm 2,80 ~ \mathrm{cm}\), les autres raies étant au-delà de la pellicule.
Question
En réalité, même si la fente (\(\varphi\)) est infiniment fine, les raies observées précédemment ont une certaine largeur.
Quels phénomènes, que nous négligerons dans la suite du problème, permettent d'interpréter cette observation ?
Solution détaillée
Si la fente source est infiniment fine, les maximums de lumière devraient correspondre à des raies infiniment fines mais la radiation utilisée (la raie double du sodium) est un mélange des deux longueurs d'onde et, de plus, ces deux longueurs d'onde ne sont pas parfaitement monochromatiques du fait de deux phénomènes. Du fait que la désexcitation des atomes de sodium n'est pas instantanée (une inégalité de Heisenberg entraîne une légère indétermination sur la longueur d'onde émise) et du fait que les atomes de sodium ne sont pas immobiles mais animés de différentes vitesses (un effet Doppler différent pour chacun d'eux entraîne une nouvelle indétermination sur la longueur d'onde). Ces deux phénomènes, faibles seront négligés dans la suite.
Question
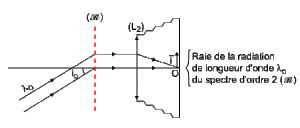
Le spectrographe étant encore en incidence normale, la source de lumière monochromatique est remplacée par une source de lumière blanche (les radiations émises ont des longueurs d'onde dans le vide comprises entre \(400 ~ \mathrm{nm}\) et \(760 ~ \mathrm{nm}\) environ).
Décrire brièvement ce que l'on observe en surface sensible. Le spectre d'ordre 2 est-il vu en totalité ?
Solution détaillée
En lumière blanche, le point central correspond à un maximum de lumière pour toutes les radiations. Il est donc blanc. En dehors du point central, chaque radiation donne sa propre alternance de lumière-obscurité. Si on calcule \(x_1\), \(x_2\) et \(x_3\) pour \(\lambda = 400\) et \(760 ~ \mathrm{nm}\), on voit que tout le spectre 2 n'entre pas sur la pellicule et qu'il commence à être recouvert par le spectre 3.
Question
On tourne l'ensemble réseau - appareil photographique pour que le milieu de la raie de longueur d'onde \(\lambda_0\) dans le vide du spectre d'ordre 2 coïncide avec le centre \(O\) de la surface sensible. L'angle d'incidence \(i\) prend alors la valeur particulière \(i_0\).
Exprimer \(i_0\) en fonction de \(n\) et de \(\lambda_0\).
Exprimer l'abscisse \(x\) de la raie de longueur d'onde \(\lambda\) du spectre d'ordre 2, en fonction de \(n\), \(\cos i'\), \(f_2\) et de la différence \((\lambda - \lambda_0)\).
Application numérique : en utilisant les valeurs déjà fournies en Q3 et Q5, calculer :
la valeur de l'angle \(i_0\)
les valeurs de l'angle d'émergence \(i'\) correspondant aux limites extrêmes du spectre visible d'ordre 2.
Compte tenu de ces derniers résultats numériques, peut-on dire que, aux approximations habituelles près, la différence \((\lambda - \lambda_0)\) est proportionnelle à \(x\) ?
Solution détaillée
On oriente l'ensemble réseau - appareil photo de façon à annuler l'angle \(i^,_2\) pour la radiation \(\lambda_0\). L'angle d'incidence vaut alors \(i_0\). On a donc \(\sin i_0 = 2 n \lambda_0\) soit \(i_0 = 19,3^{\circ}\). Pour la radiation de longueur d'onde \(\lambda\), on a alors \(\sin i^,_2 = 2 n \lambda - \sin i_0 = 2n (\lambda - \lambda_0)\) et
\(x_2 = f_2 ~ \tan i^,_2 = \frac{2n ~ f_2 ~ (\lambda - \lambda_0)}{\sqrt{1 ~ - ~ 4 n^2 (\lambda - \lambda_0)^2}}\)
Pour \(\lambda = 400 ~ \mathrm{nm}\) et \(760 ~ \mathrm{nm}\), on trouve \(i^,_2 = 6,08^{\circ}\) et \(5,49^{\circ}\). Dans les deux cas, le \(\cos i^,_2\) au dénominateur diffère peu de 1. On peut donc écrire \(x_2 \approx 2n ~ f_2 ~ (\lambda - \lambda_0)\) c'est-à-dire que la différence \(\lambda - \lambda_0\) est proportionnelle à \(x\).
Question
On tourne l'ensemble réseau - appareil photographique pour que le milieu de la raie de longueur d'onde \(\lambda_0\) dans le vide du spectre d'ordre 2 coïncide avec le centre \(O\) de la surface sensible. L'angle d'incidence \(i\) prend alors la valeur particulière \(i_0\).
En réalité, la largeur \(l\) de la fente \((\varphi)\) du collimateur n'est pas négligeable et, par suite, les rayons incidents au réseau \(R\) ne sont pas rigoureusement parallèles : le faisceau incident possède une "ouverture angulaire".
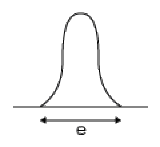
Montrer que, par suite, toute raie du spectre normal d'ordre \(k = 2\) , de longueur d'onde \(\lambda\), et d'abscisse \(x\), possède une largeur \(e\).
Exprimer \(e\) en fonction de \(\alpha\), \(f_2\) et \(\cos i_0\).
En déduire que deux raies de longueur d'onde \(\lambda\) et \(\lambda + \Delta \lambda\) ne sont discernables dans le spectre normal d'ordre 2 que si \(\Delta \lambda\) est au moins égal à une valeur minimum que l'on exprimera en fonction de \(\alpha\), \(n\) et \(\cos i_0\).
Application numérique :
\(\alpha = 2 . 10^{-3} ~ \mathrm{rad}\)
Calculer \(e\) et la valeur minimum de \(\Delta \lambda\).
Solution détaillée
Si l'on tient compte de la largeur de la fente, les rayons incidents n'ont pas tous la même direction. A partir de la relation \(\sin i + \sin i' = 2 n \lambda\), on peut écrire \(\cos i + \cos i' \frac{\mathrm d i'}{\mathrm d i} = 0\)
Mais \(i = i_0\) et \(\cos i' \approx 1\) donc \(\mathrm d i' = - \cos i_0 ~ \mathrm d i\) d'où \(\mathrm d x = - \cos i_0 ~ f_2 ~ \mathrm d i\) .
\(\mathrm d i\) étant compris entre \(- \alpha / 2\) et \(\alpha / 2\), la largeur d'une raie est donc \(e = \cos i_0 ~ f_2 ~ \alpha\)
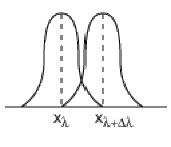
On peut dire que deux raies de longueur d'onde \(\lambda\) et \(\lambda + \Delta \lambda\) sont discernables si \(x_{\lambda + \Delta \lambda} - x_{\lambda} > \frac{e}{2}\). On en tire que \(\Delta \lambda > \frac{\cos i_0}{4 n} \alpha\). Avec les données, on calcule que \(e = 0,15 ~ \mathrm{mm}\) et \(\Delta \lambda > 1,7 ~ \mathrm{nm}\).