Le champ électrostatique E

Contrairement à la force électrostatique \(\vec F = q ~ \vec E\) dont le point d'application est la position de la charge \(q\), le champ \(\vec E\) peut être défini en tout point \(M\) quelconque de l'espace (sauf sur la source).

\(\vec E = \frac{Q}{4 \pi \epsilon_0 r^2} \vec u\)

• Son module dépend des coordonnées du point \(M\) auquel on le définit puisqu'il est inversement proportionnel au carré de la distance par rapport à la charge source \(Q\)

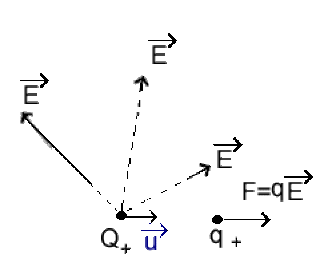
• Sa direction est radiale : elle passe toujours par la charge source \(Q_+\)

• Son sens est tel que :

  • \(\vec E\) s'éloigne des sources \(Q\) positives ( \(\vec E\) colinéaire à \(\vec u\) )

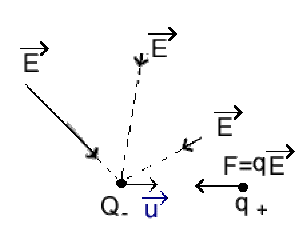
  • \(\vec E\) est dirigé vers les sources \(Q\) négatives ( \(\vec E\) opposé à \(\vec u\) )