Circulation de E
Définition
Soit un champ électrostatique \(\vec E\) créé par une charge source.
Soit une charge cible \(q\) placée dans ce champ.
Elle subit une force électrostatique \(\vec F = q ~ \vec E\).
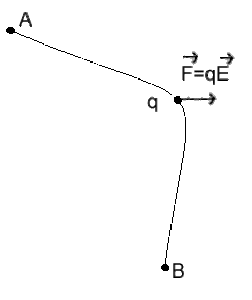
La circulation du vecteur champ \(\vec E\) d'un point \(A\) à un point \(B\) est le travail par unité de charge effectué par la force électrostatique \(q\vec E\) lorsque son point d'application se déplace du point \(A\) au point \(B\) dans le champ \(\vec E\).
\(\displaystyle{C_{AB} = \frac{\int_A^B q\vec E.\mathrm d \vec M}{q} = \int_A^B \vec E.\mathrm d \vec M}\)
Exemple de calcul
Dans l'expression de la circulation d'un vecteur \(\vec E\) le long d'un contour \(AB\), \(M\) est un point variable du contour \(AB\). \(\vec E\) est l'expression du vecteur \(\vec E\) au point \(M\). \(\mathrm d \vec M\) est l'expression d'un déplacement infinitésimal du point \(M\) sur le contour \(AB\). Suivant le type de problème étudié, \(\mathrm d \vec M\) doit être exprimé en coordonnées cartésiennes, polaires, cylindriques ou sphériques.
Propriétés
La circulation du champ \(\vec E\) créé par une charge ponctuelle entre 2 points \(A\) et \(B\) est de façon générale :
\(\displaystyle{C_{AB} = \int_A^B \frac{Q}{4 \pi \epsilon_0 r^2}\mathrm d r = \frac{Q}{4 \pi \epsilon_0 r_A}~-~\frac{Q}{4 \pi \epsilon_0 r_B}}\)
Démonstration :
Le système formé par la charge ponctuelle \(Q\) présente une symétrie sphérique . En coordonnées sphériques, un déplacement élémentaire \(\mathrm d \vec M\) s'ecrit :
\(\mathrm d \vec M =\mathrm d_r ~ \vec {u_r}~+~r\mathrm d_{\theta} ~ \vec {u_{\theta}}~+~r\sin{\theta}~\mathrm d_\phi ~ \vec {u_\phi}\)
\(\displaystyle{C = \int_A^B \vec E.\mathrm d \vec M = \int_A^B \frac{Q}{4 \pi \epsilon_0 r^2} ~ \vec {u_r} \big(\mathrm d_r ~ \vec {u_r}~+~r\mathrm d_{\theta} ~ \vec {u_{\theta}}~+~r\sin{\theta}~\mathrm d_\phi ~ \vec {u_\phi}\big) = \int_{r_A}^{r_B}\frac{Q}{4 \pi \epsilon_0 r^2}\mathrm d r}\)
car le produit scalaire \(\vec {u_r}.\vec {u_r} = 1\) et les produits croisés \(\vec {u_r}.\vec {u_\theta} = 0~\) et \(~\vec {u_r}.\vec {u_\phi} = 0\)
\(\displaystyle{C = \frac{Q}{4 \pi \epsilon_0} \int_{r_A}^{r_B} \frac{\mathrm d r}{r^2} = \frac{Q}{4 \pi \epsilon_0} \Big[-\frac{1}{r}\Big]_{r_A}^{r_B}}\)
\(\displaystyle{C = \frac{Q}{4 \pi \epsilon_0} \Big(\frac{1}{r_A}-\frac{1}{r_B}\Big)}\)
Le théorème de superposition démontre que pour une source quelconque le champ de vecteurs \(\vec E\) résulte de la superposition de champs créés par différentes charges sources ponctuelles. On peut donc énoncer la propriété générale suivante : la circulation de \(\vec E\) n'est fonction que des coordonnées du point de départ et d'arrivée indépendamment du chemin suivi.
En particulier, la circulation sur un contour fermé (\(A\) et \(B\) confondus) est nulle :
\(\displaystyle{\oint \vec E.\mathrm d \vec M = 0}\)