Le condensateur plan
On appelle condensateur plan l'ensemble formé par deux conducteurs limités par deux surfaces planes et parallèles.
Supposons d'abord que les surfaces planes des armatures aient des dimensions infinies. Il est évident par raison de symétrie que le champ électrique aurait une direction perpendiculaire à ces surfaces. En outre, la densité superficielle de charge aurait la même valeur en tous les points de la surface d'une armature. Dans le cas réel, si la distance entre les armatures est petite relativement à leurs dimensions, le champ électrique et la densité de charge ne seront changés que sur les bords. Nous négligerons ces "effets de bords" en supposant :
que le champ électrique est partout perpendiculaire aux surfaces planes des armatures. Les lignes de champ sont donc des segments rectilignes perpendiculaires à ces surfaces.
que la densité superficielle de charge est constante sur la face plane de chaque armature.
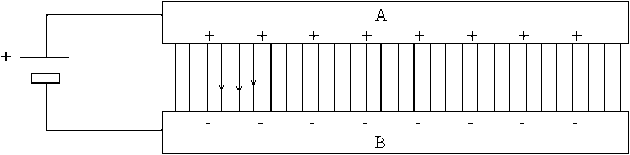
Nous avons représenté ci-après la coupe transverse d'un condensateur plan montrant les lignes de champ qui partent de la face plane de l'armature \(\mathrm A\) chargée positivement et arrivent sur la face plane de l'armature \(\mathrm B\) chargée négativement. Sur cette figure, les armatures sont des plaques, mais l'essentiel est que les faces en regard soient planes et parallèles. Il passe une ligne de champ par chaque point de l'espace compris entre les armatures et toutes ces lignes ne sont évidemment pas tracées.
La démonstration que nous allons effectuer comprend 4 parties.
a) Les quantités d'électricité réparties sur les faces planes des armatures ont des valeurs opposées :
\(Q_A= - Q_B\)
Démonstration :
Désignons respectivement par \(\sigma_A\) et \(\sigma_B\) les densités superficielles de charge sur les faces planes des armatures \(\mathrm A\) et \(\mathrm B\). Appliquons le théorème des éléments correspondants à un tube de champ élémentaire, c'est-à-dire à un tube de champ très étroit. Notons \(\mathrm d S\) l'aire de la section droite de ce tube de champ. Les deux éléments correspondants portent les charges \(\sigma_A . \mathrm d S\) et \(\sigma_B . \mathrm d S\) qui ont des valeurs opposées :
\(\sigma_A . \mathrm d S = - \sigma_B . \mathrm d S\)
d'où \(\sigma_A = - \sigma_B\)
L'armature \(A\) porte la charge :
\(\displaystyle{Q_A = \sum_i \sigma_A ~ \mathrm d S_i}\)
La somme \(\displaystyle{\sum}\) étant faite pour tous les éléments de surface \(\mathrm d S_i\) qui composent la face plane de l'armature \(\mathrm A\). Comme la densité de charge \(\sigma_A\) est constante, on peut la mettre en facteur dans cette somme et il devient :
\(Q_A = \sigma_A ~ \sum \mathrm d S_i\) .
Soit \(Q_A = \sigma_A~S\) ,
en notant \(S\) l'aire de la face plane de l'armature \(A\), on obtient de même :
\(Q_B =\sigma_B~S\)
Et il résulte de \(\sigma_A = - \sigma_B\) que :
\(Q_A = -Q_B\)
b) Le champ électrique est uniforme :
\(E = \frac{\sigma_A}{\epsilon_0}\)
Démonstration :
Pour calculer le champ électrique en un point \(P\), on considère un tube de champ élémentaire comprenant le point \(P\) et on ferme ce tube d'une part par une section droite passant par le point \(P\), d'autre part, par une surface \(\Sigma\) située dans l'armature \(\mathrm A\). On applique le théorème de Gauss à cette surface fermée.
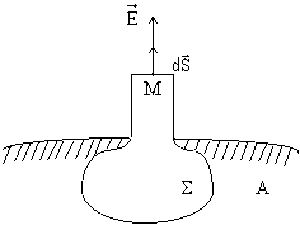
La quantité d'électricité dans le volume délimité par cette surface se trouve sur la face de l'armature \(\mathrm A\). Elle vaut : \(\mathrm d Q = \sigma_A . \mathrm d S\) en désignant par \(\mathrm d S\) la section constante du tube de champ.
Le flux \(\Phi\) du champ électrique vaut donc :
\(\Phi = \frac{\sigma_A ~ . ~ \mathrm d S}{\epsilon_0}\)
Les flux à travers le tube de champ et à travers la surface \(\Sigma\) sont nuls. Il reste le flux à travers la section du tube de champ passant par le point \(P\). Le vecteur élément de surface \(\mathrm d \vec S\) et le champ électrique ont même direction et même sens. Le flux vaut :
\(\Phi = \vec E . \mathrm d \vec S = E ~ \mathrm d S\)
On obtient donc :
\(E ~ \mathrm d S = \frac{\sigma_A ~ . ~ \mathrm d S}{\epsilon_0}\)
\(E = \frac{\sigma_A}{\epsilon_0}\)
Le champ électrique a partout la même valeur.
c) Le champ électrique est proportionnel à la d.d.p. entre les armatures
\(E = \frac{V_A - V_B}{d}\)
Démonstration :
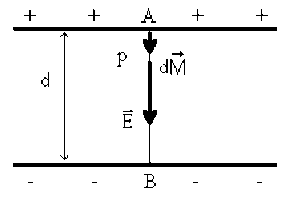
La d.d.p. est égale à la circulation du champ électrique le long d'une ligne de champ depuis le point \(\mathrm A\) sur la surface du conducteur chargé positivement jusqu'au point \(\mathrm B\) sur la surface du conducteur chargé négativement (voir la figure).
On a : \(\displaystyle{V_A - V_B = - \int_ \mathrm B^ \mathrm A \vec E . \mathrm d \vec M}\) . Or, le champ électrique \(\vec E\) et le vecteur déplacement élémentaire \(\mathrm d \vec M\) ont même direction.
D'où : \(\vec E . \mathrm d \vec M = E . \mathrm d M\)
Comme \(E\) est constant :
\(\displaystyle{V_A - V_B = \int_ \mathrm A ^ \mathrm B E . \mathrm d M = E \int_ \mathrm A^ \mathrm B \mathrm d M}\)
Comme \(\mathrm d M\) est la distance \(d\) des deux conducteurs il vient : \(V_A - V_B = E~d\).
Soit :
\(E = \frac{V_A - V_B}{d}\)
d) La quantité d'électricité portée par une armature est proportionnelle à la d.d.p.
\(Q_A = \epsilon_0 \frac{S}{d} (V_A - V_B)\)
D'où
\(C = \frac{Q}{V_A - V_B} = \epsilon_0 \frac{S}{d}\)
Démonstration :
Les résultats précédents permettent de calculer la quantité d'électricité portée par une armature. Ainsi, l'armature \(A\) au potentiel le plus élevé, a la quantité d'électricité positive :
\(Q_A = \sigma_A.S\)
Eliminons \(\sigma_A\) de cette expression au moyen de la relation \(E = \frac{\sigma_A}{\epsilon_0}\), il vient :
\(Q_A = \epsilon_0 . E . S\)
Puis en tenant compte de la relation \(E = \frac{\sigma_A}{\epsilon_0}\), on obtient :
\(Q_A = \epsilon_0 \frac{S}{d} (V_A - V_B)\)
D'où :
\(C = \frac{Q}{V_A - V_B} = \epsilon_0 \frac{S}{d}\)