Visibilité des franges

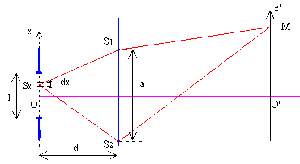
Considérons le dispositif des fentes d'Young vu précédemment, la fente étant considérée jusqu'alors comme infiniment fine.

Donnons maintenant une largeur \(l\) à cette fente. Elle peut être décomposée en une juxtaposition de fentes élémentaires de largeur infiniment fine \(\mathrm{d}x\), parallèles mais incohérentes.

Avec \(1 \ll d\), la différence de marche s'écrit :

\(\begin{array}{c c l} d = (S_xS_2M) - (S_x S_1M) &=& (S_xS_2 + S_2M) - (S_xS_1 + S_1M) \\ & =& (S_xS_2 - S_xS_1) + (S_2M - S_1M) \end{array}\)

Par analogie avec les calculs vus précédemment :

\(S_xS_2 - S_xS_1 = \frac{X.S_1S_2}{d}\) d'où

\(\delta = S_1S_2 ( \frac{x}{d} + \frac{x'}{D}) = a(\frac{x}{d} + \frac{x'}{D})\) avec  \(S_1S_2 = a\) (distance entre le sources secondaires) .

En supposant la source mère d'intensité uniforme sur toute la surface et émettant de manière identique dans toutes les directions, on peut écrire que l'éclairement \(\mathrm{d}I\) au point \(M\) de l'écran, dû à la source \(Sx\) , est proportionnel :

• à la largeur de la source élémentaire \(S_x\)

• au terme d'interférences \((1 + \cos \frac{2 \pi \delta}{\lambda})\) propre à cette fente source éclairant \(S_1\) et \(S_2\) de manière cohérente.

\(\mathrm{d}I = K.\mathrm{d}x(1 + \cos \frac{2 \pi \delta}{\lambda})\)

En tenant compte de la largeur totale \(l\) de la source:

\(\begin{array}{rcl} I_M &=&\displaystyle{ \int_{-\frac{1}{2}}^{+\frac{1}{2}} K \mathrm{d}x . \left[1+ \cos 2 \pi \frac{S_1S_2}{\lambda}\left(\frac{x'}{D} + \frac{x}{d}\right)\right] }\\\\ &=& \displaystyle{K \left[1+ \frac{\lambda d}{\pi a} \sin \frac{\pi l a}{\lambda} \cos 2 \pi \frac{a}{\lambda} \frac{x'}{D}\right]} \\\\ &=& \displaystyle{K. l \left[1 + \frac{\lambda d}{\pi a l} \sin \frac{\pi l a}{\lambda} \cos 2 \pi \frac{a}{\lambda} \frac{x'}{D}\right]} \end{array}\)

de manière de plus compacte et en posant : \(K. l = I_0\) et \(\frac{\pi l a}{\lambda d} = u\)

\(I_M = I_0 [1 + \frac{\sin u}{u} \cos 2 \pi \frac{a x'}{\lambda D}]\)

lorsque \(l\) tend vers \(0\) alors \(u\) tend vers \(0\) et \(\frac{\sin u}{u} \to 1\).

La relation, décrivant l'intensité au point \(M\), devient celle donnée dans le cas fictif d'une fente source \(S\) infiniment fine.

La visibilité se définit par:

\(V = \frac{I_{max} - I_{min}}{I_{max} + I_{min}}\)

ce qui, dans notre cas, donne:

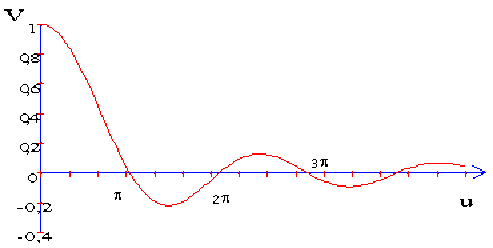
\(V =\frac{\sin u}{u}\)

Pour fixer un ordre de grandeur, la valeur \(\mathrm{0,5}\) de la visibilité correspond à :

\(u = 1,9 \quad avec \quad u = \frac{\pi a l}{\lambda d} \Rightarrow l \cong \frac{1}{30} \mathrm{ mm } \quad si \quad d = 10 \mathrm{ cm }, a = 1 \mathrm{ mm }, \lambda = 0,5.10^{-6} \mathrm{ m }\)

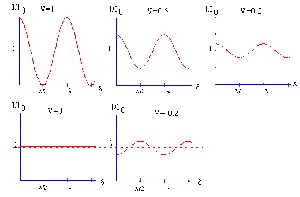
On remarque que pour :

• \(u = k \pi\) la visibilité est nulle et on ne distingue plus les franges.

• \(p < u <2 \pi\) la visibilité prend une valeur négative.

La frange centrale n'est plus brillante mais sombre: en effet \(I_{min}\) devient supérieur à \(I_{max}\), les franges sombres remplacent les franges brillantes avec un contraste fortement diminué. L'interfrange n'est pas modifiée.

Pratiquement chaque source mère \(S_x\) crée son propre système d'interférences; on observe donc sur l'écran la superposition de systèmes d'interférences décalés, donc une figure globale d'interférences de moins en moins détectable au fur et à mesure que la fente s'élargit.