Puissance - Travail - Energie
Partie
Question
Travaux et Energie potentielle (2ème partie) (**)
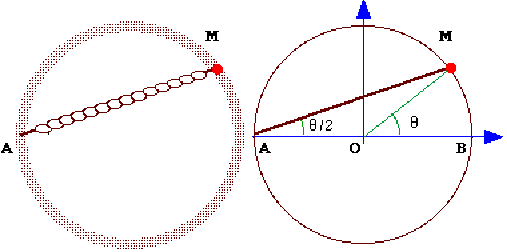
Une masse m se déplace sans frottement sur un rail circulaire de rayon \(R\) situé dans un plan vertical dans le champ de pesanteur. Le diamètre horizontal du cercle est \(AB\), son centre est \(O\) et la position \(M\) de la masse est repérée par l'angle \(\theta\) que font \(OB \textrm{ et }OM\). La masse est accrochée à un ressort de raideur \(k\), de longueur nulle au repos et fixé en \(A\). Le système a, par définition, une énergie potentielle nulle en \(A\).
a) Donner l'expression de l'énergie potentielle du système en fonction de \(R, q, g, m \textrm{ et }k\).
b) Que représente le gradient de l'énergie potentielle ?
c) Calculer la composante tangentielle de la résultante des forces qui s'exercent sur la masse. Montrer que cette composante s'annule pour deux positions que l'on précisera.
Préciser pourquoi ces positions sont des positions d'équilibre.
Aide simple
Les énergies potentielles d'origines diverses s'ajoutent. Sur un cercle, en coordonnées polaires, la variable r est constante...
Solution détaillée
a) La variation de l'énergie potentielle DEp au cours d'un déplacement fini est :
égale et de signe opposé au travail de la résultante des forces appliquées \(\overrightarrow F\);
ou encore égale au travail de la force opposée à la force résultante (-\(\overrightarrow F\))
ou encore égale au travail d'un opérateur qui s'oppose à la résultante des forces
ou encore égale au travail d'un opérateur qui s'oppose à chacune des forces en jeu,
ce qui a été étudié dans la première partie.
\(\displaystyle{\Delta E_p=\Delta E_{\textrm{pesanteur}}+\Delta E_{\textrm{élastique}}}\)
L'énergie potentielle est prise nulle en \(A (E_p(A)= 0)\) , ce qui signifie :
- l'origine de l'énergie potentielle de pesanteur prise sur le diamètre AB
- l'origine de l'énergie potentielle élastique prise nulle en \(A\), puisque le ressort est de longueur nulle en \(A\); alors, l'expression de l'énergie potentielle \(E_p = E_p(M) - E_p(A) = \Delta E_p\). On reprend donc les expressions de chacun des termes contribuant à l'énergie potentielle totale :
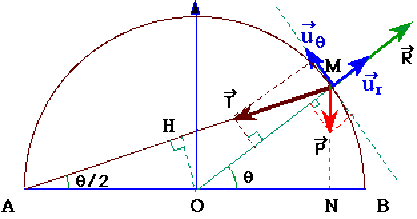
\(\displaystyle{\Delta~E_{\textrm{pesanteur}}=mgh\textrm{ où }h=MN=R\sin\theta}\)
soit encore\( \displaystyle{\Delta E_{\textrm{pesanteur}} = mgR \sin\theta}\)
\(\displaystyle{\Delta E_{\textrm{élastique}}=\frac{1}{2}kx^2}\) où \(x\) est l'allongement soit ici la longueur \(AM\) ;
or, \(\displaystyle{AM=2AH=2R\cos\frac{\theta}{2}}\) et par suite,
\(\displaystyle{\Delta E_{\textrm{élastique}}=\frac{1}{2}k(2R\cos\frac{\theta}{2})^2=kR^2(1+\cos\theta)}\)
\(\displaystyle{E_p=\Delta E_p=mgR\sin\theta+kR^2(1+\cos\theta)}\)
b) Le gradient de \(E_p\) au point \(M\), lorsqu'il existe, est par définition, l'opposé de la résultante des forces appliquées au système. Dans ce cas, à savoir le poids de la masse \(\overrightarrow P\) , la tension du ressort\( \overrightarrow T\) et la réaction \(\overrightarrow R\) du rail :
\(\displaystyle{\overrightarrow{\textrm{grad}}_ME_p=(-\sum\overrightarrow F)=-(\overrightarrow P+\overrightarrow T+\overrightarrow R)}\)
c) La composante tangentielle de la résultante des forces Fq s'obtient à partir de l'expression de l'énergie potentielle :
\(\displaystyle{\overrightarrow{\textrm{grad}}_ME_p=-\frac{\delta E_p}{\delta r}\overrightarrow u_r-\frac{1}{r}\frac{\delta E_p}{\delta\theta}\overrightarrow u_\theta=F_r\overrightarrow u_r+F_\theta\overrightarrow u_\theta}\)
Mais le calcul de \(\Delta Ep\) a eu lieu sur le cercle; par suite \(r = \textrm{Cste} = R\) donc la dérivée partielle devient une dérivée totale sur le cercle :
\(\displaystyle{F_\theta=-\frac{1}{r}\frac{\delta E_p}{\delta\theta}=-\frac{1}{r}\frac{\textrm dE_p}{\textrm d\theta}=-\frac{1}{r}\frac{\textrm d}{\textrm{d}\theta}[mgR\sin\theta+kR^2(1+\cos\theta)]}\)
\(\displaystyle{F_\theta=-mg\cos\theta+Rk\sin\theta}\)
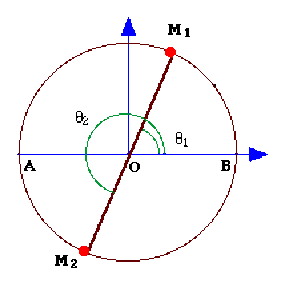
Cette composante s'annule pour \(\displaystyle{\textrm{tg }\theta=\frac{mg}{Rk}}\) . Il y a deux solutions\( \theta_1\) et \(\theta_2\) telles que et
\(\displaystyle{\theta_1 =\textrm{Arc tg }\frac{mg}{Rk}\textrm{ et } \theta_1=\theta_2+\pi}\).