Fonctions circulaires directes
Périodicité, parité, symétrie, domaine d'étude
Soit une fonction \(f\) définie sur \(D_{f} \in \mathbb{R}\) et à valeurs dans \(\mathbb{R}\).
La fonction \(f\) est périodique, de période \(T\) ( ou \(T-\textrm{ p\'eriodique}\)) si :
\(\forall x \in D_{f} ~f(x + T) = f (x)\)
Son graphe est invariant par des translations de vecteurs \(kT\vec{i}\) ( \(k \in Z\); \(\vec{i}\) vecteur unitaire sur l'axe des abscisses).
La fonction \(f\) est paire, si :
\(\forall x \in D_{f} \quad(-x) \in D_{f} \textrm{ et }f (-x) = f (x)\)
Son graphe admet l'axe \(Oy\) comme axe de symétrie.
Plus généralement : si
\(\forall x' \in D_{f}, \forall x'' \in D_{f} : x' + x'' = a \Rightarrow f (x') = f (x'')\) alors le graphe admet la droite d'équation \(x = a/2\) pour axe de symétrie.
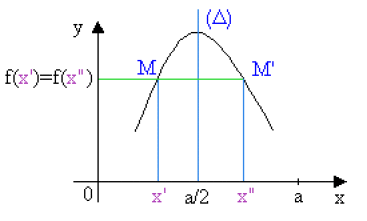
\(\left\{\begin{array}{lll} x'+x'' = a \\ f(x') = f(x'') \end{array}\right.\)
L'axe \(x=a/2\) est axe de symétrie
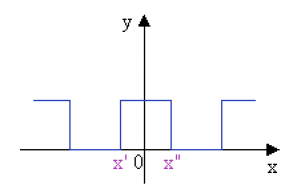
\(\left\{\begin{array}{ccc} x'+x'' = 0 &\Rightarrow &x' = -x''\\ f(x') = f(x'') &\Rightarrow & f(x') = f(x'') = f(-x') \end{array}\right.\)
Fonction paire
L'axe \(Oy\) est axe de symétrie
La fonction \(f\) est impaire, si
\(\forall x \in D_{f} \quad(-x) \in D_{f} \textrm{ et } f (-x) = - f (x)\)
Son graphe admet l'origine des coordonnées comme centre de symétrie.
Plus généralement : si
\(∀x' \in D_{f}, ∀x'' \in D_{f} : x' + x'' = a \Rightarrow f (x') + f (x'') = b\) alors le graphe admet le point de coordonnées \((a/2 ; b/2)\) pour centre de symétrie.
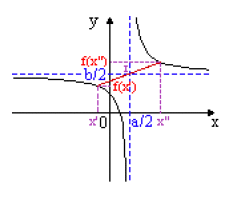
\(\left\{\begin{array}{lll} x'+x'' = a \\ f(x') + f(x'') = b \end{array}\right.\)
L'axe \(I(a/2, b/2)\) est axe de symétrie
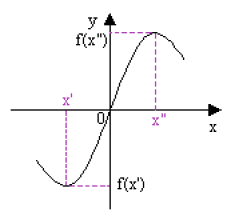
\(\left\{\begin{array}{ccc} x'+x'' = 0 &\Rightarrow & x' = -x''\\ f(x') + f(x'') = 0&\Rightarrow& f(x') = - f(x'') =- f(-x') \end{array}\right.\)
Fonction impaire
L'origine des axes de coordonnées est centre de symétrie
Le domaine d'étude \((D_{e})\) d'une fonction sera réduit suivant les particularités que peut présenter cette fonction. La périodicité permet d'étudier \(f\) sur un intervalle de longueur \(T\) par exemple \([ 0; T]\) ou \([ -T/2 ; T/2]\). Les symétries réduisent de moitié cet intervalle
Fonction sinus de x : sin x
La fonction sinus, notée \(\sin\), est :
définie sur \(\mathbb{R}\)
\(2\pi\) - périodique : \(\sin(x + 2\pi) = \sin x\)
impaire : \(\sin(-x) = - \sin x\)
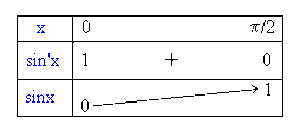
Le domaine d'étude se réduit à \(D_{e} = [0 , \pi/2]\)
car le graphe de la fonction sinus, admet un axe de symétrie d'équation \(x = \pi/2\).
(En effet : \(x' + x'' = \pi \Rightarrow \sin (x') = \sin (\pi - x'') = \sin(x'')\) )
La fonction dérivée \(\sin' x = \cos x\) étant positive sur \(D_{e}\), la fonction \(\sin x\) est croissante.
Représentation graphique de sinus
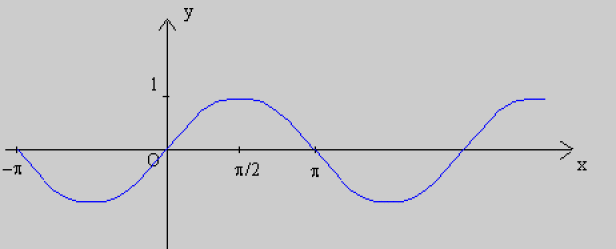
Fonction cosinus de x : cos x
La fonction cosinus, notée \(\cos\), est :
définie sur \(\mathbb{R}\)
\(2\pi\) - périodique : \(\cos(x + 2\pi) = \cos x\)
paire : \(\cos(-x) =\cos x\)
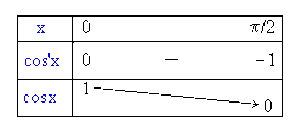
Le domaine d'étude se réduit à \(D_{e} = [0 , \pi/2]\)
car le graphe de la fonction cosinus, admet un centre de symétrie de coordonnées \((\pi/2,0)\).
(En effet : \(x' + x'' = \pi \Rightarrow \cos (x') = \cos (\pi - x'') = -\cos(x'') \textrm{ et } \cos(x') + \cos(x'') = 0\) )
La fonction dérivée \(\cos' x = -\sin x\) étant négative sur \(D_{e}\), la fonction \(\cos x\) est décroissante.
Représentation graphique de cos
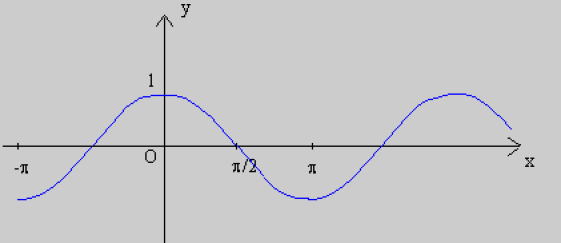
Fonction tangente de x : tan x
La fonction tangente, notée \(\tan,\) est :
définie sur \(\mathbb{R} -\{\pi/2 + k\pi\} (k \in \mathbb{Z}) \textrm{ par } \tan x = \sin x/\cos x.\)
\(\pi\) - périodique : \(\tan(x + \pi) = \tan x\)
impaire : \(\tan(-x) =-\tan x\)
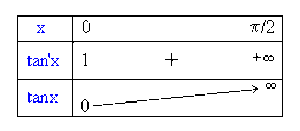
Le domaine d'étude se réduit à \(D_{e} = [0 , \pi/2[\)
La fonction dérivée \(\tan' x = 1+\tan^{2}x = 1/\cos^{2}x\) étant négative sur \(D_{e}\), la fonction \(\tan x\) est croissante.
Représentation graphique de tangente
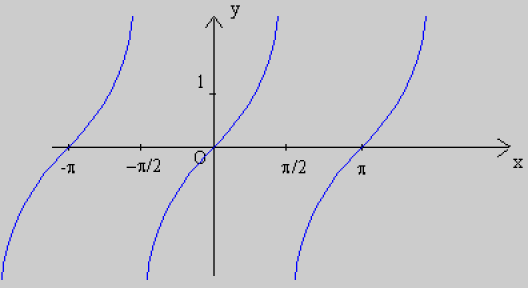
Fonction cotangente de x : cotan x
La fonction cotangente, notée \(\textrm{cotan}\), est :
définie sur \(\mathbb{R} -\{\ k\pi\} (k \in \mathbb{Z}) \textrm{ par } \textrm{cotan } x = 1/\tan x = \cos x/ \sin x\)
\(\pi\) - périodique : \(\textrm{cotan}(x + \pi) = \textrm{cotan }x\)
impaire : \(\textrm{cotan }(-x) =-\textrm{ cotan }x\)
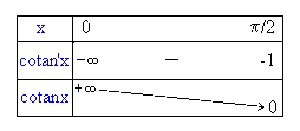
Le domaine d'étude se réduit à \(D_{e} = ]0 , \pi/2]\)
La fonction dérivée \(\textrm{cotan}' x = -(1+\tan^{2}x) = -1/\sin^{2}x\) étant négative sur \(D_{e}\), la fonction \(\textrm{cotan }x\) est décroissante.
Représentation graphique de cotangente
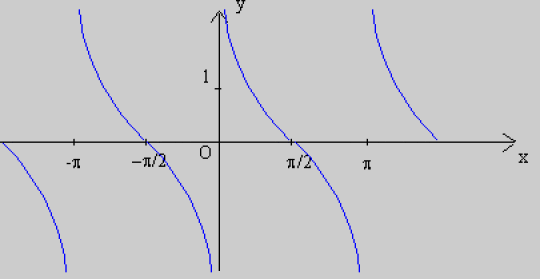
Inversion des fonctions trigonométriques
\(\forall (\alpha,\beta)\in \mathbb{R}^{2}\)
\(\sin \alpha = \sin \beta \Leftrightarrow \left\{\begin{array}{lr} \alpha = \beta &[2\pi]\\ \alpha = \pi-\beta &[2\pi]\end{array}\right.\)
Exemple : Inversion des sinus
Résoudre : \(\sin \left(3x - \frac{\pi}{2}\right) =\frac{\sqrt{3}}{2}\)
sachant que \(\frac{\sqrt{3}}{2} = \sin \frac{\pi}{3}\), l'équation à résoudre devient
\(\sin \left(3x-\frac{\pi}{2}\right) = \sin \frac{\pi}{3}\)
d'où les solutions :
\(\begin{array}{lll}3x - \frac{\pi}{2} = \frac{\pi}{3} + 2k \pi \Leftrightarrow x = \frac{5 \pi}{18} + \frac{2k\pi}{3} \\\textrm{ et } \\3x - \frac{\pi}{2} =\pi -\frac{\pi}{3} + 2k \pi \Leftrightarrow x = \frac{7 \pi}{18} + \frac{2k\pi}{3} \end{array}\) \(k\in \mathbb{Z}\)
\(\forall (\alpha,\beta)\in \mathbb{R}^{2}\)
\(\cos \alpha = \cos \beta \Leftrightarrow \left\{\begin{array}{lr} \alpha = \beta &[2\pi]\\ \alpha = -\beta &[2\pi]\end{array}\right.\)
Exemple : Inversion des cosinus
Résoudre : \(\cos \left(2x - \frac{\pi}{3}\right) =\frac{\sqrt{2}}{2}\)
sachant que \(\frac{\sqrt{2}}{2} = \cos \frac{\pi}{4}\), l'équation à résoudre devient
\(\cos \left(2x-\frac{\pi}{3}\right) = \cos \frac{\pi}{4}\)
d'où les solutions :
\(\begin{array}{lll}2x - \frac{\pi}{3} = +\frac{\pi}{4} + 2k \pi \Leftrightarrow x = \frac{7 \pi}{24} + k\pi \\\textrm{ et } \\2x - \frac{\pi}{3} = -\frac{\pi}{4} + 2k \pi \Leftrightarrow x = \frac{\pi}{24} + k\pi \end{array}\) \(k\in \mathbb{Z}\)
\(\forall (\alpha, \beta)\in \left(\mathbb{R} - \left(\frac{\pi}{2} + k \pi\right)\right)^{2} k\in\mathbb{Z}\)
\(\tan \alpha = \tan \beta \Leftrightarrow \alpha = \beta \qquad [\pi]\)
Exemple :
Résoudre : \(\tan \left(x - \frac{\pi}{3}\right) =\frac{\sqrt{3}}{3}\)
sachant que \(\frac{\sqrt{3}}{3} = \tan \frac{\pi}{6}\), l'équation à résoudre devient
\(\tan \left(x-\frac{\pi}{3}\right) = \tan \frac{\pi}{6}\)
d'où les solutions :
\(x - \frac{\pi}{3} = \frac{\pi}{6} +k \pi \Leftrightarrow x = \frac{\pi}{2} + k \pi \quad k\in\mathbb{Z}\)
\(\forall (\alpha, \beta)\in \left(\mathbb{R} - k \pi\right)^{2} k\in\mathbb{Z}\)
\(\textrm{cotan }\alpha = \textrm{cotan }\beta \Leftrightarrow \alpha = \beta \qquad [\pi]\)
Exemple :
Résoudre : \(\textrm{cotan }\left(x + \frac{\pi}{6}\right) =1\)
sachant que \(1 = \textrm{cotan }\frac{\pi}{4}\), l'équation à résoudre devient
\(\textrm{cotan }\left(x+\frac{\pi}{6}\right) = \textrm{cotan }\frac{\pi}{4}\)
d'où les solutions :
\(x + \frac{\pi}{6} = \frac{\pi}{4} +k \pi \Leftrightarrow x = \frac{\pi}{12} + k \pi \quad k\in\mathbb{Z}\)