Puissance de matrice [Calcul matriciel]

Puissance de matrice

Soit la matrice $A = \begin{pmatrix} 1 & 0 & 3 \\ 0 & 3 & 1 \\ 3& 1 & 0\end{pmatrix}$ ,

calculer $A^{2}$ et $A^{3}$ .

Effectuer les produits suivants :

$\color{blue}[A^{2}] = [A]~\textrm{x}~[A]$

$\color{blue}[A^{3}] = [A^{2}]~\textrm{x}~[A]$

Un calcul classique des produits de matrices conduit aux résultats suivants :

$A^{2} = \begin{pmatrix} 10 & 3 & 3 \\ 3 & 10 & 3 \\ 3 & 3 & 10 \end{pmatrix}$

$A^{3} = \begin{pmatrix} 19 & 12 & 33 \\ 12 & 33 & 19 \\ 33 & 19 & 12 \end{pmatrix}$

Calculons $A^{2} = A × A$ en positionnant les matrices sous la forme suivante :

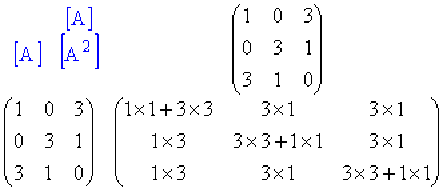
$\color{red} A^{2} = \begin{pmatrix} 10 & 3& 3 \\ 3 & 10 & 3 \\ 3 & 3& 10\end{pmatrix}$

Calculons $A^{3} = A^{2} × A$ en positionnant les matrices sous la forme suivante :

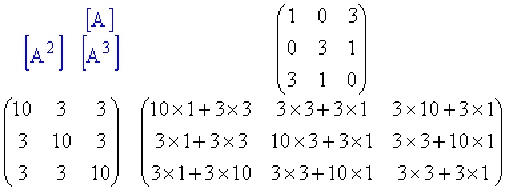
$\color{red} A^{3} = \begin{pmatrix} 19 & 12 & 33 \\ 12 & 33 & 19 \\ 33 & 19 & 12 \end{pmatrix}$