Adaptation en puissance
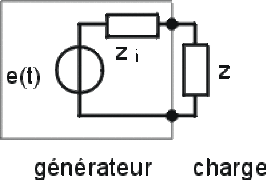
Soit un générateur de f.é.m. telle que \(\underline e(t)=E_m\textrm{e}^{j\omega t}=E\sqrt{2}\textrm{e}^{j\omega t}\), ayant pour impédance interne complexe : \(\underline Z_i = R_i + j.X_i\) et alimentant une charge d'impédance complexe : \(\underline Z =R + j.X\) ; on dira qu'il y a adaptation en puissance entre le générateur et la charge si la puissance dissipée dans la charge est maximale. La puissance complexe correspondante a pour expression : `
\(\displaystyle{\underline p=\frac{\underline Z.\underline i.\underline i^*}{2}=\frac{\underline Z}{2}.\frac{\underline e}{\underline Z+\underline Z_i}.\frac{\underline e^*}{\underline Z^*+\underline Z^*_i}=E^2\frac{R+jX}{(R+R_i)^2+(X+X_i)^2}}\)
d'où la puissance active \(P\), partie réelle de \(\displaystyle{\underline p :P=E^2\frac{R}{(R+R_i)^2(X+X_i)^2}}\):
qui sera maximale si :
\(X + X_i = 0\iff X=-X_i\) et, cette condition étant remplie :
\(\displaystyle{\frac{d}{dR}\Big(\frac{R}{(R+R_i)^2}\Big)=C}\)
L'existence de ce maximum est évidente : quand la première condition est remplie, on a : \(\displaystyle{P=\frac{R.E^2}{(R+R)^2_i}}\) dont la valeur, positive, tend vers zéro pour les valeurs limites de \(R ( R \to 0 \textrm{ et } R \to\infty)\).
D'après le théorème de Rolle, la fonction \(P(R)\) présente au moins un maximum dans l'intervalle \([0, +\infty[\) .
Recherchons ce maximum.
\(\displaystyle{\frac{d}{dR}\Bigg(\frac{R}{(R+R_i)^2}\Bigg)=\frac{1}{(R+R_i)^2}-\frac{2R}{(R+R_i)^3}=\frac{R-R_i}{(R+R_i)^3}}\)
La dérivée s'annule pour \(R = R_i\). La puissance transférée du générateur à la charge est donc maximale si l'impédance complexe de cette charge vérifie les deux conditions : \(R = R_i \textrm{ et } X = -X_i\) ; autrement dit, si \(\underline Z = \underline Z^*_i\).
La puissance fournie par un générateur à une charge est maximale si leurs impédances complexes sont des complexes conjugués.
La valeur du maximum est :
\(\displaystyle{P_{\textrm{max}}=\frac{E^2}{4R_i}=\frac{E^2_m}{8R_i}}\)
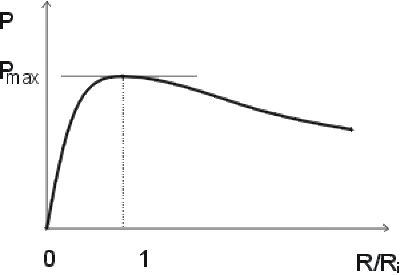
l'allure de la courbe \(P(R)\) est donnée ci-dessous :