Résolution
La résolution d'une équation différentielle du premier ordre peut se faire en deux étapes. Il faut d'abord chercher une solution de l'équation dite "homogène" ou "sans second membre":
\(\displaystyle{\tau\frac{\mathrm ds}{\mathrm dt}+s(t)=0}\)
On cherche ensuite une solution particulière de l'équation complète, du même type que \(f[e(t)]\) (solution constante si \(f[e(t)]\) a une valeur constante, polynôme du même ordre s'il s'agit d'un polynôme de \(t\), fonction périodique, etc.) La solution générale de l'équation complète s'obtient en faisant la somme de la solution de l'équation homogène et de la solution particulière. (pour la démonstration, voir " Outils Mathématiques pour la Physique ", équations différentielles du premier ordre à coefficients constants). La valeur des constantes d'intégration est donnée par les conditions initiales.
Méthode :
Exercice résolu :
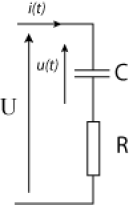
A la date \(t=0\), on applique instantanément, aux bornes d'un condensateur non chargé et monté en série avec un conducteur ohmique, une différence de potentiel constante \(\mathrm U\). Déterminer l'équation de la tension \(u(t)\) aux bornes du condensateur.
Solution :
Aux bornes du générateur on peut écrire: \(u(t)+\mathrm R.i(t)=\mathrm U\). Aux bornes du condensateur on peut écrire: \(q(t)=\mathrm C.u(t)\). Comme il n'y a pas de dérivation, l'intensité du courant est la même partout, donc est liée à la charge du condensateur par :
\(\displaystyle{i(t)=\frac{\mathrm dq}{\mathrm dt}=C.\frac{\mathrm du}{\mathrm dt}}\) On obtient donc l'équation différentielle: \(\displaystyle{u(t)+\mathrm{R.C}\frac{\mathrm du}{\mathrm dt}=\mathrm U}\), qui montre que le circuit étudié est un circuit du premier ordre de constante de temps \(\tau=\mathrm{RC}\)
Résolution de l'équation homogène :
En supprimant le second membre, on obtient l'équation : \(\displaystyle{u(t)+\mathrm{R.C}\frac{\mathrm du}{\mathrm dt}=0}\) qui peut aussi s'écrire : \(\displaystyle{u(t)+\tau\frac{\mathrm du}{\mathrm dt}=0}\), soit, en séparant les variables \(u\) et \(t\) : \(\displaystyle{\frac{\mathrm du}{u}=\frac{\mathrm dt}{\tau}}\); \(\displaystyle{\frac{\mathrm du}{u}}\) étant la différentielle du logarithme népérien de \(u\ln(u)\), la solution est : \(\displaystyle{\ln(u)=-\frac{t}{\tau}+\mathrm{constante}}\), équivalente à :
\(\displaystyle{u(t)=\mathrm A.e^{-\frac{t}{\tau}}}\)
où A est une constante qu'il faudra déterminer par la suite.
Solution particulière de l'équation complète:
\(\displaystyle{u(t)+\mathrm{R.C}\frac{\mathrm du}{\mathrm dt}=\mathrm U}\)
comme \(U\) a une valeur constante, on cherche une solution particulière \(u(t)\) constante; alors sa dérivée \(\displaystyle{\frac{\mathrm du}{u}}\) est nulle et en reportant cette valeur dans l'équation on obtient:
\(u(t)=\mathrm U\)
la solution complète de l'équation différentielle est donc: \(\displaystyle{u(t)=\mathrm A.e^{-\frac{t}{\tau}}+\mathrm U}\)
il reste à déterminer la valeur de \(\mathrm A\) en utilisant les conditions initiales ; à \(t=0\), le condensateur est déchargé, donc la tension aux bornes de ce condensateur est nulle : \(u(0)=0\), qui, reporté dans l'équation précédente, conduit à :
\(\displaystyle{u(0)=\mathrm A.e^{-\frac{0}{\tau}}+\mathrm U}\) soit : \(0=\mathrm A+\mathrm U\), d'où \(\mathrm A=-\mathrm U\) et finalement \(u(t)\):
\(\displaystyle{u(t)=\mathrm U(1-e^{-\frac{t}{\tau}})}\)
la tension aux bornes du condensateur passe donc progressivement de 0 à \(\mathrm U\)en suivant une loi exponentielle.
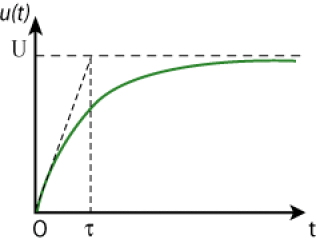
La dérivée par rapport au temps de \(u(t)\) est : \(\displaystyle{\frac{\mathrm du}{\mathrm dt}=\mathrm U.\frac1{\tau}.e^{-\frac{t}{\tau}}}\), dont la valeur pour \(t=0\) est donc \(\displaystyle{\left(\frac{\mathrm du}{\mathrm dt}\right)_0=\frac{\mathrm U}{\tau}}\), et dont la limite pour \(t\) tendant vers l'infini est nulle. La tangente à l'origine à la courbe \(u(t)\) coupe donc l'asymptote horizontale \(u(t)=\mathrm U\) pour \(t=\tau\); à cette date, la tension \(u(t)\) vaut \(u(t)=\mathrm U(1-e^{-1})\approx\mathrm{0,63 U}\)