Ondes électromagnétiques

Dans le cas de réflexion totale de l'onde incidente (pas d'onde transmise à l'extérieur du système), l'onde réfléchie qui prend naissance à la limite du système (en \(z = z_1\)) est déterminée à tout instant par le fait que l'amplitude totale de la vibration doit être nulle.

Si par exemple la limite du système est en \(z = z_1 = L\) :

\(F(\omega . t - K . L) + G(\omega . t + K . L) = 0\)

avec \(F(\omega . t - K . L) = A_p . \cos (\omega . t - K . L)\)

\(\Rightarrow ~~~~ G(\omega . t + K . L) = - A_p . \cos (\omega . t - K . L)\)

La vibration réfléchie \(G\) qui prend naissance en \(z = z_1\) est donc harmonique, comme l'incidente.

La vibration réfléchie en \(z = z_1\) joue ainsi le rôle de source. Cependant, alors que la vibration de la source qui créé l'onde progressive s'exprime \(A_p . \cos (\omega.t)\), la "source" qui créé l'onde réfléchie a une amplitude qui varie selon : \(- A_p . \cos (\omega.t - K.z_1)\)

On doit donc poser que la réflexion peut introduire un déphasage \(\alpha\) de l'onde incidente, de sorte que la propagation de l'onde réfléchie s'exprime :

En \(z = z_1\), l'amplitude de l'onde réfléchie est donc : \(G(\omega.t + K.z_1) = A_r . \cos (\omega.t + K.z_1 + \alpha)\)

En particulier : à l'instant \(t = 0\) et en \(z = z_1\), l'amplitude de l'onde réfléchie est alors :

\(G(K.z_1) = A_r . \cos(K.z_1 + \alpha)\)

avec \(G(K.z_1) = - A_p . \cos(-K.z_1) = - A_p . \cos(K.z_1)\)

\(\Rightarrow ~~~~ A_r . \cos (K.z_1 + \alpha) = - A_p . \cos(K.z_1)\)

En supposant par exemple que les coefficients d'amplitudes \(A_p\) et \(A_r\) soient tous deux positifs, on obtient une solution possible telle que :

Dans ces conditions, l'onde réfléchie se propage sous la forme :

Avec ces conditions de réflexion totale (traduites ici par \(A_r = A_p = A\) et \(\alpha = \pi\)) la vibration résultante sera :

Cette expression représente une onde stationnaire, i.e. une onde caractérisée par l'existence

• de nœuds de vibration [pour \(\cos(Kz) = 0\)] et

• de ventres de vibration [pour \(\cos (Kz) = \pm 1\)]

Pour que s'établissent des ondes stationnaires dans un système, la relation ci-dessus doit être compatible avec les conditions aux limites du système.

Considérons un système dont les extrémités, totalement réfléchissantes, sont situées en

\(z = z_0\) et \(z = z_1\)

Si, par exemple, la première extrémité du système est un ventre de vibration, on aura \(\cos (Kz_0) = 1\) ce qui autorise alors à choisir l'origine des ordonnées en \(z_0 = 0\).

Si, par contre, le début du système est un nœud de vibration, on aura \(\cos (Kz_0) = 0\), et l'on pourra par exemple prendre l'origine des ordonnées de sorte que \(Kz_0 = \frac{\pi}{2}\) , soit :

\(z_0 = \frac{\pi}{2 K}\) avec \(K = \frac{2 \pi}{\lambda} ~~~~ \Rightarrow ~~ z_0 = \frac{\lambda}{4}\)

Si la deuxième extrémité du système est également un noeud de vibration, on aura également \(\cos (K.z_1) = 0\), d'où : \(K.z_1 = \frac{(2n + 1) . \pi}{2}\)

Si les deux extrémités du système sont des noeuds de vibration, la longueur \(L\) du système est donc reliée à la longueur d'onde par :

\(K . z_1 - K . z_0 = \frac{(2n + 1) . \pi}{2} - \frac{\pi}{2} = n . \pi\)

soit : \(L = z_1 - z_0 = \frac{n . \pi}{K} = n . \frac{\lambda}{2}\)

Pour que l'une des extrémités soit un nœud de vibration et l'autre un ventre de vibration, on trouve de la même façon que la longueur du système doit être :

\(L = (2n + 1) . \frac{\lambda}{4}\)

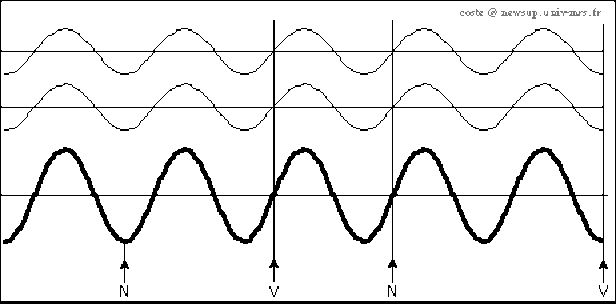
Sous réserve que soient satisfaites ses conditions aux limites, le système peut être le siège d'une onde stationnaire. Cette onde stationnaire s'exprime par une combinaison linéaire d'ondes harmoniques progressive et régressive de même amplitude, de même fréquence, de vitesses égales en valeur absolue et de sens opposés.

Contrôlez sur ces simulations les résultats qui ont été établis ci-dessus.

Considérons par exemple une onde progressive :

et une onde régressive : \(G(\omega.t+K.z) = A_r.\cos (\omega.t + K.z + \alpha)\) produite par réflexion, pour laquelle, comme précédemment, la réflexion introduit un déphasage \(\alpha = \pi\). Alors :

On suppose que les conditions de réflexion permettent l'existence d'une onde transmise à l'extérieur du système, de sorte que l'onde réfléchie a une amplitude \(A_r\) inférieure à l'amplitude \(A_p\) de l'onde incidente.

L'onde progressive peut s'exprimer :

\(F(\omega.t - K.z) = [ A_p- A_r ] \cos (\omega.t - K.z) + A_r . \cos (\omega.t - K.z)\)

et l'onde résultante :

\(F(\omega.t - K.z) + G(\omega.t + K.z) = [A_p - A_r ].\cos (\omega.t - K.z) + A_r.[\cos (\omega.t - K.z) - \cos (\omega.t + K.z)]\)

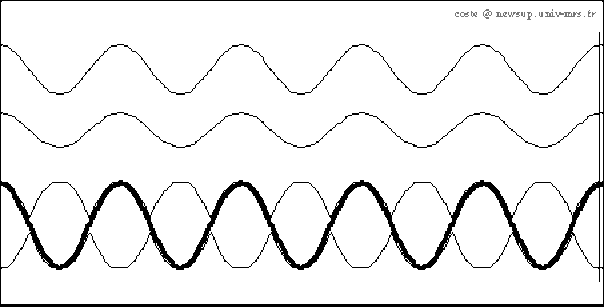
Dans ces conditions, l'onde résultante est la somme :

• d'une onde progressive : \([A_p - A_r] . \cos (\omega.t - K.z)\) et

• d'une onde stationnaire : \(A_r.[\cos (\omega.t -K.z) - \cos (\omega.t + K.z)]\)

On peut dire que ce système est le siège d'un "taux d'ondes stationnaires", ou d'ondes "pseudo-stationnaires". Il ne pas confondre ces vibrations avec les vibrations stationnaires : en effet ici, les positions des noeuds et des ventres de vibrations ne sont pas des points fixes, mais se translatent dans le sens imposé par l'onde qui a la plus grande amplitude (ici l'onde incidente).