Réaction d'ordre 1 [Approche formelle des lois de vitesse d'ordre simple]

Réaction d'ordre 1

Loi de vitesse

L'expression de la vitesse est proportionnelle à la concentration d'un réactif \(\textrm A\) :

\(\mathbf{\textrm v=-\frac{\textrm dC_\textrm A}{\textrm dt}=k.C_\textrm A}\) qui s'intègre en :

\(\mathbf{\ln\frac{C_\textrm A}{C_{\textrm A0}}=-k.t}\) ou \(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k.t} k \textrm{en s}^{-1}\)

\(C_{\textrm A0}\) étant la concentration initiale de \(\textrm A\) et \(C_\textrm A\) sa concentration au temps \(t\).

Si vous désirez consulter des détails concernant l'intégration, cliquez ici^[1].

De l'expression précédente, on tire facilement la relation qui permet de calculer la concentration de \(\textrm A\) à un instant \(t\) :

\(\mathbf{C_\textrm A=C_{\textrm A0}.\exp(-k.t)}\)

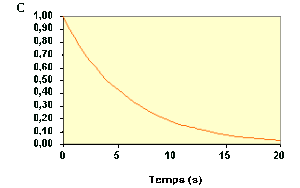
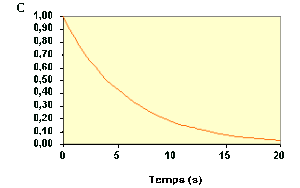
La variation de \(C_\textrm A\) au cours du temps suit donc une courbe de décroissance exponentielle :

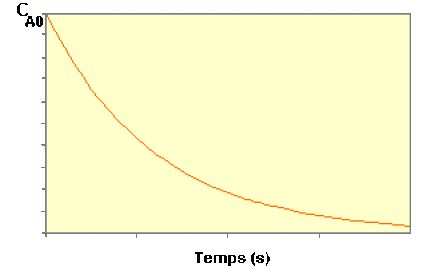
Cliquez ici^[2] pour voir d'autres formes de la loi de vitesse.

Remarque :

Dans ce qui précède, on a utilisé la vitesse volumique \(\textrm v\), on aurait tout aussi bien pu utiliser la vitesse \(\omega\) exprimée à partir de l'avancement de réaction \(\xi\) .

Temps de demi-vie

Le temps de demi-vie (ou période) \(t_{\frac12}\) est égal à \(\mathbf{t_{\frac12}=\frac{\ln2}{k}}\) et est donc indépendant de la concentration initiale.

Si vous désirez consulter un rappel concernant la période, cliquez ici^[3].

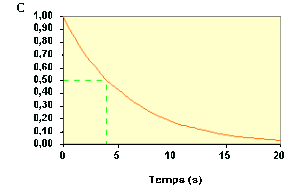
Le temps de demi-vie peut se déterminer facilement à partir de la courbe \(C_\textrm A = f (t)\) .

Le fait que le temps de demi-vie soit indépendant de la concentration initiale est caractéristique des réactions d'ordre 1.

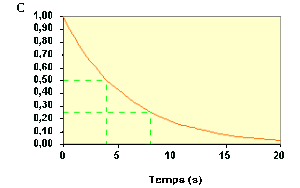
A partir d'une même courbe \(C_\textrm A = f (t)\), on peut déterminer plusieurs temps de demi-vie successifs.

Il est même possible de déterminer des temps de demi-vie qui se chevauchent.

Vérification de l'ordre 1 d'une réaction

Position du problème :

On étudie une réaction et on désire s'assurer qu'elle obéit bien à une loi du premier ordre. Si c'est bien le cas, on veut déterminer son coefficient de vitesse. Selon les cas, on peut effectuer cette vérification à partir :

des valeurs des temps de demi-vie
des valeurs des vitesses correspondantes à différentes concentrations
des valeurs de concentration mesurées au cours du temps.

Le premier cas est le plus simple, il suffit de s'assurer que le temps de demi-vie est indépendant de la concentration.

La vérification à partir des vitesses est un peu plus simple qu'à partir des concentrations (3ème cas), mais risque d'être moins précise (car en général les vitesses sont déterminées avec moins de précision que les concentrations).

Explication :

Vérification à partir des temps de demi-vie

Dans certains cas, on connaît le temps de demi-vie pour plusieurs expériences effectuées avec des concentrations initiales différentes. Si ces expériences ont toutes été effectuées dans les mêmes conditions (notamment de température), le fait que le temps de demi-vie soit constant suffit à établir que la réaction est du premier ordre. Il est également possible de vérifier la constance du temps de demi-vie sur une seule expérience.

Vérification à partir des vitesses

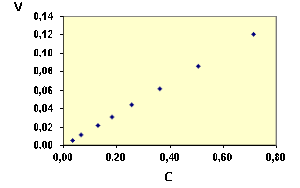
On suppose que l'on dispose de valeurs de la vitesse de réaction \(\textrm v\) correspondantes à plusieurs valeurs de la concentration \(C_\textrm A\).

Pour vérifier la loi de vitesse \(\mathbf{\textrm v=-\frac{\textrm dC_\textrm A}{\textrm dt}=k.C_\textrm A}\) il suffit de vérifier que la vitesse \(\textrm v\) est proportionnelle à \(C_\textrm A\).

On peut le faire soit graphiquement soit numériquement.

Vérification à partir des concentrations

On suppose que l'on dispose de valeurs de la concentration \(C_\textrm A\) pour diverses valeurs du temps.

Pour vérifier la loi de vitesse, on utilisera sa forme intégrée \(\mathbf{\ln\frac{C_\textrm A}{C_{\textrm A0}}=-k.t}\).

On peut le faire soit graphiquement soit numériquement.

De manière graphique on porte \(\ln C_\textrm A\) en fonction de \(t\) et on s'assure que les points s'alignent sur une droite.

La pente de la droite est égale à \(– k\) et l'ordonnée à l'origine est égale \(\ln C_{\textrm A0}\).

On peut aussi porter \(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}}\) en fonction de \(t\). Les points doivent s'aligner sur une droite de pente \(k\) passant par l'origine.

De manière numérique, on calcule le coefficient de vitesse \(k\) par la relation \(\mathbf{k=\frac{1}{t}\times\ln\frac{C_{\textrm A0}}{C_\textrm A}}\) pour les divers couples de valeurs de \(C_\textrm A , t\) et on s'assure que ces valeurs sont sensiblement constantes.

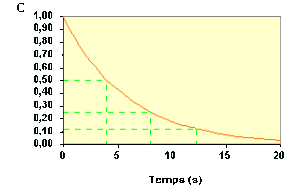
Exemple : Vérification de l'ordre 1 à partir du temps de demi-vie

La variation de concentration du réactif \(\textrm A\) au cours du temps d'une réaction est représentée sur cette figure.

Déterminons graphiquement la date qui correspond à \(C=\frac{C_0}{2}\). On trouve : \(t_1 = 4\textrm{ s}\).

Donc la première période : \(t_{\frac12}= t_1 = 4\textrm{ s}\)

Déterminons la date qui correspond à \(C = \textrm{0,25}\). On trouve \(t_2 = \textrm{8,2 s}\).

La deuxième période vaut donc : \(t_2 – t_1 = \textrm{8,2} – \textrm{4,0} = \textrm{4,2 s}\).

On peut considérer que ces deux valeurs (4,0 et 4,2) sont sensiblement égales.

Cherchons à le confirmer en déterminant la date pour \(C = \textrm{0,125}\). On trouve : \(t_3 = \textrm{12,2 s}\) .

La troisième période vaut donc : \(t_3 – t_2 = \textrm{12,2} – \textrm{8,2} = \textrm{4,0 s}\).

Ainsi, la valeur du temps de demi-vie déterminée pour différentes concentrations est sensiblement constante \(t_1 = \textrm{4,0 s}\) ; \(t_2 – t_1 = \textrm{4,2 s}\) et \(t_3 – t_2 = \textrm{4,0 s}\).

Ceci permet de conclure que la réaction obéit à une loi d'ordre 1.

Remarque :

Dans cet exemple, les temps de demi-vie sont très voisins. Il peut se faire que, compte tenu des erreurs expérimentales, on trouve des temps de demi-vie légèrement différents bien que la réaction soit du premier ordre.

Exemple : Vérification de l'ordre 1 à partir des vitesses

A partir de cette courbe, on peut déterminer graphiquement, la vitesse de la réaction pour différents instants.

On a trouvé les résultats suivants :

t (s)	2	4	6	8	10	12	16	20
v mol.L^-1.s^-1	0,121	0,086	0,061	0,044	0,031	0,022	0,011	0,006

Pour chaque point, on relève aussi la concentration, que l'on porte dans le même tableau.

t (s)	2	4	6	8	10	12	16	20
v mol.L^-1.s^-1	0,121	0,086	0,061	0,044	0,031	0,022	0,011	0,006
C mol.L^-1	0,071	0,051	0,036	0,026	0,018	0,013	0,007	0,003

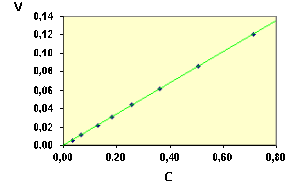
On peut faire la vérification de la relation \(\textrm v = k. C_\textrm A\) soit numériquement, soit graphiquement.

De manière numérique, on calcule \(k\) pour les diverses valeurs de \(C_\textrm A\) et on s'assure que ces valeurs sont sensiblement constantes. On trouve les valeurs suivantes :

On observe que pour les derniers points les valeurs s'écartent de celles obtenues pour les premiers points ; il est facile de voir que la précision sur ces deux derniers points est sensiblement moins grande.

De manière graphique, on porte \(\textrm v\) en fonction de \(C_\textrm A\) et on constate que les points s'alignent bien sur une droite passant par l'origine

La droite passant par ces points a une pente égale au coefficient de vitesse.

On trouve une pente égale à : 1,7 d'où \(k = \textrm{1,7 s}^{-1}\).

Remarque :

Dans cet exemple, les points représentant la vitesse en fonction du temps sont parfaitement alignés. Il n'en sera pas toujours de même avec des valeurs expérimentales à cause de l'imprécision sur la détermination de la vitesse.

Exemple : Vérification de l'ordre 1 à partir des concentrations

La variation de concentration du réactif \(\textrm A\) au cours du temps d'une réaction est représentée sur la figure ci-dessous :

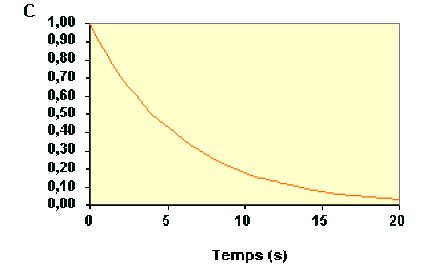
La loi de vitesse sous sa forme intégrée s'écrit :

\(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k.t} k \textrm{en s}^{-1}\)

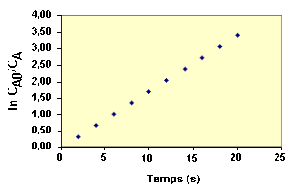
En portant \(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}}\) en fonction du temps, on doit trouver une droite de pente \(k\).

La figure suivante montre le graphe obtenu à partir de 10 points de la courbe précédente. On constate que les points sont bien alignés.

Exemple : Autre exemple de vérification de l'ordre 1 à partir des concentrations

La variation de concentration du réactif \(\textrm A\) au cours du temps d'une réaction est représentée sur la figure ci-dessous :

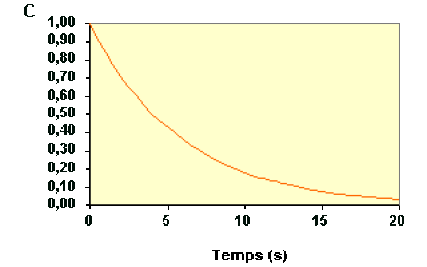
La loi de vitesse sous sa forme intégrée s'écrit :

\(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k.t } k \textrm{en s}^{-1}\)

On peut donc calculer la valeur de \(k\) pour chaque point par la relation :

\(\mathbf{k=\frac{1}{t}\ln\frac{C_{\textrm A,0}}{C_\textrm A}} k \textrm{en s}^{-1}\)

Avec 10 points de la courbe précédente, on trouve des valeurs constantes égales à 1,7 s^-1, ce qui montre que la réaction obéit à une loi d'ordre 1.

\(k=\frac{1}{t}\ln\frac{C_{\textrm A0}}{C_\textrm A} k \textrm{en s}^{-1}\)

Avec 10 points de la courbe précédente, on trouve des valeurs constantes égales à 1,7 s^-1, ce qui montre que la réaction obéit à une loi d'ordre 1.

Remarque :

Dans cet exemple, les points représentant \(\ln\frac{C_{\textrm A0}}{C_\textrm A}\) en fonction du temps sont parfaitement alignés. Il n'en sera pas de même avec des valeurs expérimentales à cause de l'imprécision sur les mesures.

Vous pouvez voir ci-dessous différents exemples de réactions d'ordre 1 :

réactions de décomposition en phase gazeuse
réactions en solution
réactions de désintégrations nucléaires

Exemple : Réactions de décomposition en phase gazeuse

Un grand nombre de réactions de décomposition en phase gazeuse suivent une loi de vitesse du premier ordre. Citons-en quelques unes à titre d'exemple :

Décomposition de l'azométhane :

\(\mathbf{\textrm{CH}_3\textrm N_2\textrm{CH}_3 (\textrm g) = \textrm{CH}_3\textrm{CH}_3 (\textrm g) + \textrm N_2 (\textrm g)}\)

Décomposition du chlorure de thionyle :

\(\mathbf{\textrm{SO}_2\textrm{Cl}_2 (\textrm g) = \textrm{SO}_2 (\textrm g) + \textrm{Cl}_2 (\textrm g)}\)

Décomposition du pentoxyde de diazote :

\(\mathbf{\textrm N_2\textrm O_5 (\textrm g) = 2. \textrm{NO}_2 (\textrm g) + \frac{1}{2}. \textrm O_2 (\textrm g)}\)

Si ces réactions sont conduites à volume et température constants, on pourra suivre leur évolution par la variation de pression totale du système.

Exemple : Réactions en solution

Il existe aussi des réactions en solution qui suivent une loi d'ordre 1. Par exemple :

Décomposition du peroxyde d'hydrogène en solution aqueuse (eau oxygénée) :

\(\mathbf{2.\textrm H_2\textrm O_2 (\textrm{aq}) = 2.\textrm H_2\textrm O (\textrm l) + \textrm O_2 (\textrm g)}\)

Cette réaction peut être suivie en mesurant le volume de dioxygène dégagé.

Hydrolyse en milieu aqueux de certains chlorures organiques :

\(\mathbf{\textrm R-\textrm{Cl} (\textrm{aq}) + \textrm H_2\textrm O (\textrm l) = \textrm{ROH} (\textrm{aq}) + \textrm{HCl} (\textrm{aq})}\)

Cette réaction peut être suivie en dosant la quantité de \(\textrm{HCl}\) formée.

Exemple : Réactions nucléaires

Bien que les réactions nucléaires ne puissent être considérées, à proprement parler, comme des réactions chimiques, nous les évoquerons brièvement ici.

Les réactions de désintégration nucléaires obéissent à une loi d'ordre un. En général, on s'intéresse au nombre d'atomes du nucleïde considéré plutôt qu'à sa concentration.

La loi de vitesse intégrée peut alors s'écrire : \(\mathbf{\ln\frac{N_0}{N}=k.t}\)

dans laquelle \(N_0\) est le nombre d'atomes à l'instant \(t = 0\) et \(N\) le nombre d'atomes restants à l'instant \(t\). Le coefficient de vitesse est alors appelé constante de désintégration.

La vitesse de réaction (nombre de désintégrations par seconde) est appelée activité de la substance radioactive (unité dans le S.I : le becquerel, symbole Bq).

Cliquez ici^[4] si vous désirez des précisions sur les unités d'activité radioactive.

Le temps de demi-vie (ou période) est une constante caractéristique de la substance radioactive. Les périodes des éléments radioactifs varient de plusieurs ordres de grandeur.

Par exemple, le polonium 212 a une période de 3,0 x 10^-7 s tandis que celle de l'uranium 238 est de 4,5 x 10⁹ ans.

Notes

Intégration de la loi de vitesse
La loi de vitesse sous sa forme différentielle s'écrit : \(\mathbf{\textrm v=-\frac{\textrm dC_\textrm A}{\textrm dt}=k.C_\textrm A}\)
en séparant les variables, il vient : \(\mathbf{-\frac{\textrm dC_\textrm A}{C_\textrm A}=k.\textrm dt}\)
qui s'intègre en \(\mathbf{-\ln C_\textrm A=k.t+\textrm{Cte}}\)
La constante d'intégration \(\textrm{Cte}\) s'obtient avec les conditions initiales \(t = 0\) et \(C_\textrm A = C_{\textrm A0}\) d'où \(-\ln C_{\textrm A0}=\textrm{Cte}\) et la forme intégrée de la loi de vitesse :
\(\mathbf{\ln\frac{C_\textrm A}{C_{\textrm A0}}=-k.t}\) ou \(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k.t} \qquad k \textrm{en s}^{-1}\)
D'autres formes de la loi de vitesse
Parfois, il est commode d'introduire \(x\) la concentration transformée, et de poser \(a = C_{\textrm A0}\) concentration initiale. Il vient alors :
\(\mathbf{C_\textrm A=a-x \qquad \ln\frac{a}{a-x}=k.t}\)
Cette expression peut s'obtenir par substitution dans l'équation
\(\mathbf{\ln\frac{C_\textrm A}{C_{\textrm A0}}=-k.t}\) ou \(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k.t} \qquad k \textrm{en s}^{-1}\)
ou directement par intégration de la loi de vitesse qui s'écrit avec les notations proposées :
\(\mathbf{\textrm v=\frac{\textrm dx}{\textrm dt}=k.(a-x)}\)
On utilise aussi parfois la fraction transformée \(\mathbf{\alpha=\frac{x}{a}}\) d'où : \(\mathbf{\ln\frac{1}{1-\alpha}=k.t}\)
La période
Le temps de demi-vie (ou période) \(\mathbf{t_{\frac12}}\) est le temps pour lequel la concentration initiale a été divisée par deux.
Donc pour \(\mathbf{t_{\frac12}}\), \(\mathbf{C=\frac{C_0}{2}}\) en portant dans l'expression intégrée :
\(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k.t}\) on obtient \(\mathbf{\ln\frac{C_{\textrm A0}}{C_{\textrm A0}/2}=k.t_{\frac12} \Longrightarrow \ln2=k.t_{\frac12}}\)
d'où \(\mathbf{t_{\frac12}=\frac{\ln2}{k}}\)
Remarque :
Le terme "période", bien que d'un usage fréquent, n'est pas bien choisi.
En effet, le phénomène n'a rien de périodique.
On lui préférera le terme "temps de demi-vie".
Unités d'activité radioactive
L'activité d'une source radioactive se définit par le nombre de désintégrations par seconde.
L'unité dans le système international est le becquerel (symbole Bq) qui est égal à une désintégration par seconde.
Une autre unité employée couramment est le curie (symbole Ci) qui est égal à l'activité de 1g de radium 226 et qui correspond à 3,7x1010 Bq.
Dans les questions de radioprotection, on s'intéresse à la dose absorbée.
Celle-ci se mesure en gray (symbole Gy) qui est défini par l'énergie absorbée par kilogramme de masse corporelle. 1 gray = 1 J.kg-1
Le gray est l'unité du système international, mais l'unité pratique est le rad (abrégé de radiation absorbe dose) 1 rad = 10-2 J.kg-1 et 1 gray = 100 rad (rad est)
Notes bibliographiques
Antoine Henri Becquerel (1852-1908)
Marie Curie (1867-1934)
Pierre Curie (1859-1906)
Marie Curie avec son mari Pierre Curie et Henri Becquerel, étudia le phénomène de la radioactivité découvert par ce dernier. Les trois reçurent le prix Nobel de physique en 1903. Avec la découverte du radium et du polonium, elle reçut le prix Nobel de chimie en 1911. Elle fut non seulement la première femme à recevoir un prix Nobel, mais la seule à en recevoir deux ! Elle fut aussi la première femme titulaire d'une chaire à la Sorbonne.