Approche expérimentale des lois de vitesse

La vitesse des réactions chimiques dépend fortement de la température. Les études expérimentales sont donc généralement conduites à température constante.

Pour étudier l'influence de la température, on effectue plusieurs études isothermes à différentes températures.

Pour chaque température, on cherche à établir la loi de vitesse et à déterminer le coefficient de vitesse. En général, la forme de la loi de vitesse ne change pas avec la température, seule la valeur du coefficient de vitesse varie. Puis on cherche à établir la relation entre la valeur du coefficient de vitesse et la température.

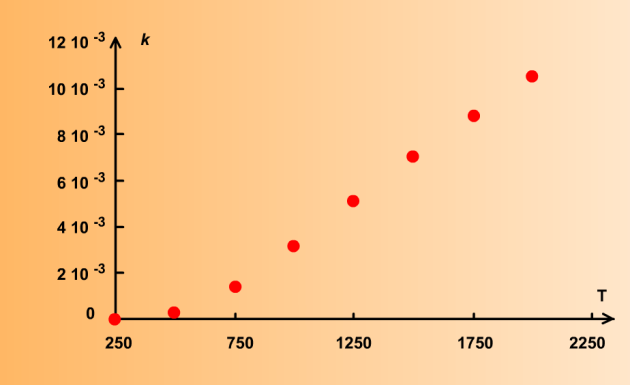
En général, le coefficient de vitesse augmente fortement avec la température, comme indiqué sur le graphe suivant :

Cependant, il existe quelques rares cas de réactions où la vitesse n'augmente pas sensiblement, voire même diminue avec la température. Ce comportement "anormal" tient au fait que ces réactions font intervenir des espèces chimiques instables qui sont dégradées à température élevée.

L'étude quantitative de la variation du coefficient de vitesse \(k\) avec la température \(T\) a permis à Svante Arrhenius de proposer en 1889 une l'équation qui porte son nom :

\(E_a\) est l'énergie d'activation de la réaction

\(A\) est le facteur préexponentiel

\(R\) est la constante des gaz parfaits (8,314 J.mol^-1.K^-1)

\(T\) la température en Kelvin

Physicien et chimiste suédois, Svante August Arrhénius (né en 1859) est l'auteur de la théorie de la dissociation électrolytique (1887) pour laquelle il reçut le Prix Nobel en 1903. Arrhénius est décédé le 2 octobre 1927, à l'âge de 68 ans.

On verra dans le prochain chapitre (Bases de la théorie - Théorie des collisions) que le facteur \(\exp\Big(-\frac{E_a}{R.T}\Big)\) représente la fraction des chocs qui se produisent entre les molécules avec une énergie supérieure à \(E_a\), d'où son nom d'énergie d'activation. Ce facteur dépend fortement de la température.

Le facteur préexponentiel \(A\), lui, dépend très peu de la température, on peut donc le considérer comme constant pour une réaction donnée (du moins dans une plage de température pas trop grande). Nous verrons également au prochain chapitre que le facteur préexponentiel \(A\) est proportionnel à la fréquence des chocs entre molécules, d'où le nom de facteur de fréquence qu'on lui donne également.

Toutes les réactions n'obéissent pas à la relation d'Arrhenius. Aussi, avant d'utiliser cette relation pour calculer la valeur du coefficient de vitesse à une température donnée, il importe donc de le vérifier. Pour ce faire, on transforme l'équation en prenant le logarithme de chaque membre :

Si une réaction obéit à la relation d'Arrhenius, les points obtenus en portant \(\ln k\) en fonction de \(\frac{1}{T}\) pour diverses expériences, doivent s'aligner sur une droite de coefficient directeur \(- \frac{E_a}{R}\) et d'ordonnée à l'origine \(\ln A\).

En reprenant les points de la figure précédente, on obtient le graphe suivant :

La valeur de l'énergie d'activation \(E_a\) que nous avons trouvée dans l'exemple précédent (\(E_a = 20 \textrm{kJ.mol}^{-1}\)) est une valeur assez faible. Certaines réactions ont une énergie d'activation plus importante, par exemple pour la réaction de décomposition de \(\textrm N_2\textrm O_5\) qui nous a servi d'exemple au début de ce chapitre \(E_a = 88\textrm{ kJ.mol}^{-1}\). Des valeurs encore plus élevées de plusieurs centaines de kJ ont été déterminées pour d'autres réactions telles que la décomposition d'hydrocarbures en phase gazeuse. La figure suivante représente la variation du coefficient de vitesse de réactions ayant un comportement d'Arrhenius pour diverses valeurs de l'énergie d'activation.

En fait sur ce graphique, on a du mal à comparer la forme des variations car les valeurs de \(k\) varient dans des ordres de grandeurs qui sont différents. On peut mieux comparer les formes en changeant d'échelle pour chaque courbe :

En tout premier lieu, il convient de s'assurer que la réaction considérée a bien un comportement d'Arrhenius.

Pour cela, nous avons vu qu'il faut disposer de plusieurs valeurs du coefficient de vitesse déterminées à des températures différentes sur une plage assez large. La vérification de l'alignement des points ( \(\ln k, \frac{1}{T}\) ) permet de déterminer la valeur de l'énergie d'activation à partir du coefficient directeur de la droite passant par ces points et le facteur préexponentiel à partir de son ordonnée à l'origine.

Si on est certain que la réaction a bien un comportement d'Arrhenius, on pourra déterminer \(E_a\) à partir de deux couples de valeurs de \(k\) et de \(T\). Considérons par exemple la réaction de décomposition en phase gazeuse de \(\textrm{HI}\) en \(\textrm I_2\) et \(\textrm H_2\) qui obéit à une loi du second ordre. On a déterminé la valeur du coefficient de vitesse à deux températures : pour \(T_1 = 1000\textrm{ K}\), \(k_1 = \textrm{0,72 s}^{-1}\) et pour \(T_2 = 1020\textrm{ K}\), \(k_2 = \textrm{1,34 s}^{-1}\).

En admettant que la réaction ait bien un comportement d'Arrhenius, on peut écrire :

En soustrayant ces deux expressions membre à membre, on obtient :

d'où l'on tire :

L'application numérique donne : \(E_a = 263 000 \textrm{J.mol}^{-1}.\textrm K^{-1}\)

On peut évidemment en déduire la valeur du facteur préexponentiel \(\mathbf{A = \textrm{4,13}. 10^{+13}\textrm{ s}^{-1}}\) (valeurs arrondies à 3 chiffres significatifs).

Arrivé à ce stade, Il vous est vivement recommandé de faire quelques exercices d'application.

Une fois les valeurs de l'énergie d'activation et du facteur préexponentiel connus, on peut les utiliser pour calculer la valeur du coefficient de vitesse à une autre température. Cependant, il faut être prudent et ne pas chercher à extrapoler les résultats à des températures trop éloignées de la plage dans laquelle on a vérifié que la réaction suivait bien la loi d'Arrhenius.

Reprenons l'exemple précédent \(\mathbf{2.\textrm{HI} = \textrm H_2 + \textrm I_2}\) et pour lequel on a trouvé : \(E_a = 263 000 \textrm{J.mol}^{-1}\textrm{.K}^{-1}\) et \(A = \textrm{4,13}.10^{+13}\textrm{ s}^{-1}\).

On peut calculer la valeur de \(k\) entre 900 K et 1100 K car les valeurs de \(E_a\) et de \(A\) ont été déterminées entre 1000 K et 1020 K, mais il serait risqué d'extrapoler beaucoup plus loin. Par exemple, pour \(T = 1050\textrm{ K}\) en appliquant directement la relation d'Arrhenius