Réactions parallèles jumelles d'ordre 1
D'une manière générale, chacune des réactions peut avoir un ordre quelconque et faire intervenir plusieurs réactifs et produits, cependant, pour simplifier nous nous limiterons à l'étude de réactions parallèles qui sont toutes d'ordre 1.
On peut les schématiser par :
\(\substack{{\displaystyle{\begin{array}{ccccc} & \textrm A & \to & \textrm P_1 \\ \textrm{et} &\textrm A & \to & \textrm P_2 \end{array}}}\\{\textrm{g\'en\'eralisable \`a }n~ \textrm{r\'eactions ...}}}\)
Approche qualitative
Avant d'aborder dans le détail l'étude analytique de la loi de vitesse, il est utile de se familiariser avec le comportement qualitatif du système cinétique.
Dans un premier temps, nous nous limiterons au cas de deux réactions.
\(\mathbf{\displaystyle{\begin{array}{ccccccc} & \textrm A & \to & \textrm P_1 \\ \textrm{et} &\textrm A & \to & \textrm P_2 \end{array}}}\)
La réactif \(\textrm A\) est consommé simultanément par les deux réactions.
Il est donc facile de comprendre que sa vitesse globale de disparition sera la somme des vitesse des deux réactions.
Par contre, chaque produit (ici \(\textrm P_1\) et \(\textrm P_2\)) est formé avec la vitesse propre de sa réaction.
La proportion des produits formés sera donc dans le rapport de ces vitesses, donc des valeurs des coefficients de vitesse.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Etude analytique de la loi de vitesse
Soit le cas simple
\(\mathbf{\displaystyle{\begin{array}{ccccccc} & \textrm A & \to & \textrm P_1 \\ \textrm{et} &\textrm A & \to & \textrm P_2 \end{array}}}\)
Toutes les deux réactions sont d'ordre un et de coefficients de vitesse respectifs \(k_1\) et \(k_2\).
Les lois de vitesse de chaque réaction considérée séparément s'écrit :
\(\mathbf{\textrm v_1=k_1.C_\textrm A \textrm{et} \textrm v_2=k_2.C_\textrm A}\)
La vitesse globale de disparition de \(\textrm A\) est la somme de ces deux vitesses, puisque \(\textrm A\) est consommé simultanément par ces deux réactions.
\(\mathbf{\textrm v=\frac{-\textrm dC_\textrm A}{\textrm dt}=\textrm v_1+\textrm v_2=k_1.C_\textrm A+k_2.C_\textrm A=(k_1+k_2).C_\textrm A}\)
En notant \(k_\textrm{obs} = k_1 + k_2\) , il vient :
\(\mathbf{\textrm v=\frac{-\textrm dC_\textrm A}{\textrm dt}=k_\textrm{obs}.C_\textrm A}\)
qui a la forme d'une loi de vitesse du premier ordre de coefficient de vitesse \(k_\textrm{obs}\) , laquelle s'intègre facilement en :
\(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k_\textrm{obs}.t}\)
D'où l'expression de la variation de \(C_\textrm A\) en fonction du temps :
\(\mathbf{C_\textrm A=C_{\textrm A0}.\exp(-k_\textrm{obs}.t)}\)
La variation de \(\textrm A\) en fonction du temps se fait donc en suivant une loi du premier ordre dont le coefficient de vitesse est la somme des coefficients de vitesses des réactions jumelles.
Ce résultat est généralisable aux cas où il y a plus de deux réactions jumelles (toutes du même ordre).
Exprimons maintenant les concentrations des produits \(\textrm P_1\) et \(\textrm P_2\) en fonction du temps.
Soient \(x_1\) et \(x_2\) les concentrations de \(\textrm P_1\) et \(\textrm P_2\) formées à un instant \(t\).
Et \(x\) la concentration de \(\textrm A\) transformée au même instant.
La stœchiométrie des réactions montre que \(x = x_1 + x_2\).
Les concentrations des différentes espèces sont donc :
A | P1 | P2 | |
|---|---|---|---|
t=0 | CA,0 | 0 | 0 |
t | CA,0-x CA,0 - (x1 + x2) | x1 | x2 |
Ceci pour des concentrations initiales en \(\textrm P_1\) et \(\textrm P_2\) nulles.
Les vitesses de chaque réactions'écrivent :
\(\mathbf{\textrm v_1=\frac{\textrm dx_1}{\textrm dt}=k_1.C_\textrm A \textrm{et} \textrm v_2=\frac{\textrm dx_2}{\textrm dt}=k_2.C_\textrm A}\)
En faisant le rapport il vient
\(\mathbf{\frac{\textrm v_1}{\textrm v_2}=\frac{\textrm dx_1}{\textrm dx_2}=\frac{k_1}{k_2}}\)
Au temps \(t =0\), on a \(x_1 = x_2 = 0\), d'où
\(\mathbf{\frac{\textrm dx_1}{\textrm dx_2}=\frac{x_1}{x_2} \Longrightarrow \frac{x_1}{x_2}=\frac{k_1}{k_2}}\)
En tenant compte de la relation \(x = x_1 + x_2\) , il vient :
\(\mathbf{x_1=\frac{k_1}{k_1+k_2}.x \textrm{et} x_2=\frac{k_2}{k_1+k_2}.x}\)
Or \(C_\textrm A = C_{\textrm A0} - x\) d'où \(x = C_{\textrm A0} - C_\textrm A\) et
\(\mathbf{x=C_{\textrm A0}.(1-\exp(-k_\textrm{obs}.t))}\)
avec \(k_\textrm{obs} = k_1 + k_2\) d'où en définitive :
\(\mathbf{x_1=\frac{k_1}{k_\textrm{obs}}.C_{\textrm A0}.(1-\exp(-k_\textrm{obs}.t))}\)
\(\mathbf{x_2=\frac{k_2}{k_\textrm{obs}}.C_{\textrm A0}.(1-\exp(-k_\textrm{obs}.t))}\)
Influence des valeurs des coefficients de vitesse sur le régime cinétique
Voyons de nouveau quelques situations typiques.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Remarques sur l'état final
Lorsque la réaction est terminée, c'est à dire lorsque le réactif est entièrement consommé, on obtient un mélange des produits dans des proportions qui dépendent du rapport des coefficients de vitesse des réactions parallèles.
Ce mélange ne doit pas être confondu avec celui obtenu par un système de réactions opposées qui conduit à un état d'équilibre. Dans le cas présent, les réactifs étant épuisés, il n'y a plus aucune transformation dans le système.
Traitement des données expérimentales
L'objectif est double :
Vérifier que la réaction obéit bien aux lois de vitesses correspondantes au schéma cinétique.
Déterminer les valeurs des coefficients de vitesse.
D'une manière générale, on analyse d'abord la variation de concentration du réactif \(\textrm A\) en fonction du temps pour déterminer \(k_\textrm{obs}\) qui est égal à la somme \(k_1 + k_2\).
Cette réaction étant globalement du premier ordre on utilise les mêmes méthodes que celles décrites dans le chapitre "Approche formelle de lois de vitesse d'ordre simple, Réactions d'ordre un" auquel on se référera si besoin.
Cependant on reprendra ici les méthodes employées sur les exemples de réactions parallèles.
Puis on exploite les données relatives à la formation des produits \(\textrm P_1\) et \(\textrm P_2\) pour déterminer la valeur du rapport \(\frac{k_1}{k_2}\) .
Selon les données dont on dispose, on utilise les lois de vitesses (voir ci-dessus Étude analytique de la loi de vitesse) sous leurs formes différentielles ou sous leurs formes intégrées .
Utilisation de la loi de vitesse sous sa forme différentielle
Les lois de vitesses s'écrivent :
\(\mathbf{\textrm v_1 = \frac{\textrm dx_1}{\textrm dt} = k_1 . C_\textrm A \textrm{et} \textrm v_2 = \frac{\textrm dx_2}{\textrm dt} = k_2 . C_\textrm A}\)
Vitesse globale de disparition de \(\textrm A\) :
\(\mathbf{\textrm V = \frac{- \textrm dC_\textrm A}{\textrm dt} = (k_1 + k_2 ) . C_\textrm A}\)
Vitesse de formation de \(\textrm P_1\) :
\(\mathbf{\textrm v_1 = \frac{-\textrm dC_{\textrm P_1}}{\textrm dt} = k_1 . C_\textrm A}\)
Vitesse de formation de \(\textrm P_2\) :
\(\mathbf{\textrm v_2 = \frac{- \textrm dC_{\textrm P_2}}{\textrm dt} = k_2 . C_\textrm A}\)
Si on a mesuré les valeurs de \(\textrm v_1\) et \(\textrm v_2\) pour diverses valeurs de \(C_\textrm A\) (soit au cours de différentes expériences avec la méthode des vitesses initiales, soit au cours d'une seule expérience en suivant la vitesse au cours du temps), il sera très facile de vérifier le modèle cinétique et de calculer les coefficients de vitesse.
Rappelons que si l'utilisation des vitesses est simple, elle conduit souvent à des résultats assez peu précis, car la détermination des vitesses (souvent effectuée par dérivation graphique des courbes concentration / temps) est délicate et imprécise.
Exemple : Utilisation des vitesses initiales
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Exemple : Utilisation des vitesses au cours du temps
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Utilisation de la loi de vitesse sous sa forme intégrée
Les lois de vitesse sous leur forme intégrée s'écrivent :
\(\mathbf{\ln\frac{C_{\textrm A0}}{C_\textrm A}=k_\textrm{obs}.t}\)
avec
\(\mathbf{\frac{x_1}{x_2}=\frac{C_{\textrm P_1}}{C_{\textrm P_2}}=\frac{k_1}{k_2}}\)
Disposant de valeurs de \(C_\textrm A\), \(C_{\textrm P_1}\), \(C_{\textrm P_2}\) pour diverses valeurs de \(t\), on détermine d'abord \(k_\textrm{obs}\) par une méthode numérique ou graphique.
Puis on vérifie que le rapport \(\frac{C_{\textrm P_1}}{C_{\textrm P_2}} = \frac{k_1}{k_2}\) est constant.
Enfin, connaissant \(k_1 + k_2\) et le rapport \(\frac{k_1}{k_2}\) on calcule séparément les valeurs de chaque coefficient de vitesse.
Exemple : Utilisation de la loi de vitesse sous sa forme intégrée
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Exemples
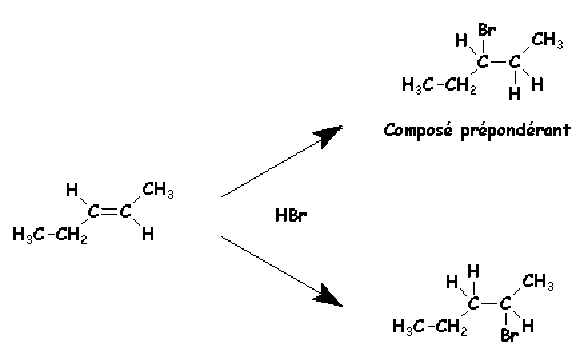
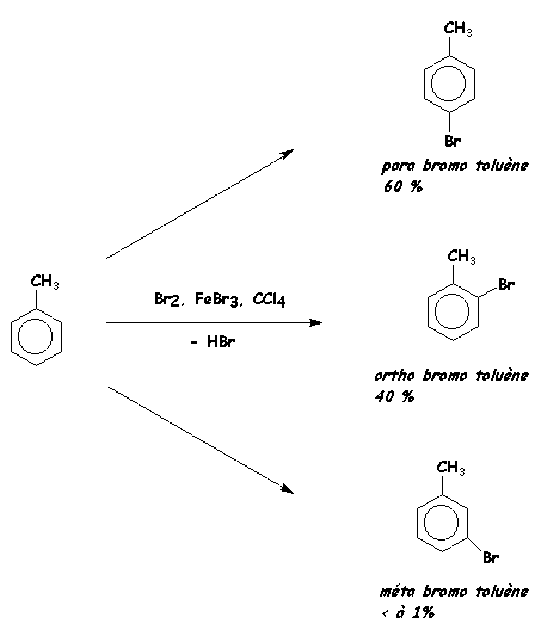
Exemple : Addition de HCl sur une liaison éhylénique non symétrique (avec dégénérescence d'ordre).