Composition de moments de liaisons
Durée : 20 mn
Note maximale : 10
Question
Sachant que le moment dipolaire de la liaison \(\mathrm{C}\mathrm{ - }\mathrm{C}\mathrm{l}\) est égal à \(\mathrm{2,2}\) Debyes et celui de la liaison \(\mathrm{C}\mathrm{-}\mathrm{H}\) à \(\mathrm{0,4}\) Debye :
a. Calculer le moment dipolaire du dichlorométhane par composition des moments de liaison.
b. Justifier l'écart entre la valeur expérimentale de ce moment dipolaire \((\mathrm{1,6}~\textrm{Debyes})\) et cette valeur calculée au moyen de la géométrie de la molécule.
(On utilisera une géométrie standard pour les calculs, sans se préoccuper de la variation des angles due à l'effet du chlore)
Solution
a. On considère le dichlorométhane dans une géométrie tétraédrique idéale. Les angles de liaisons sont de \(109°28'\). La composition des moments de liaisons \(\mathrm{C}\mathrm{-}\mathrm{C}\mathrm{l}\) et \(\mathrm{C}\mathrm{-}\mathrm{H}\) dans leur plans respectifs permet de calculer simplement la résultante, comme indiqué sur le schéma suivant :
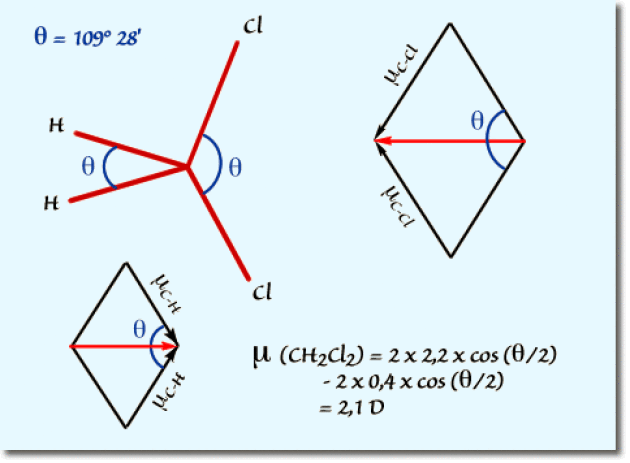
b. En fait le calcul effectué à partir du modèle tétraédrique régulier du carbone ne tient pas compte des déformations apportées à ce modèle par l'électronégativité des atomes de chlore. Les halogènes fortement électronégatifs se repoussent par interaction coulombienne dans l'espace. L'angle \(\mathrm{Cl-C-Cl}\) est par conséquent augmenté. Il en résulte une diminution de la contribution des liaisons \(\mathrm{C-Cl}\) au moment dipolair et donc une diminution du moment dipolaire global.