Energie de torsion et termes non-liés
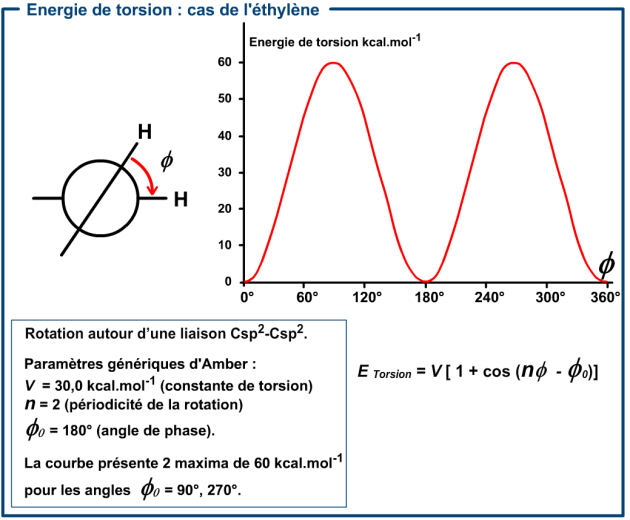
Ce terme concerne la rotation autour d'une liaison et nécessite la définition de l'angle dièdre entre deux plans eux-mêmes définis par 3 atomes liés.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Définition :
L'énergie de torsion est modélisée par une fonction périodique dont la plus simple est de la forme :
\(E_{Torsion} =\displaystyle{\sum_{i}V_{n,i}{1+\cos(n_i\mathsf{\Phi_i-\Phi_{0,i}})}} \) (Eq. 05)
\(\mathsf{\Phi_i}\) est l'angle dièdre considéré.
\(\mathsf{\Phi_{0,i}}\) est l'angle de phase.
\(n_i\) est la périodicité de la rotation.
\(V_{n,i}\) est la constante de torsion, elle s'exprime en kJ.mol-1 (ou kcal.mol-1).
Ces paramètres (\(\mathsf{\Phi_{0,i}} \mbox{,} \;n_i \mbox{ et} \; V_{n,i}\)) dépendent de la nature de la liaison et de celle des atomes liés.
Pour une molécule la sommation porte sur tous les angles dièdres de la molécule.
Exemple :
- Cas d'une liaison simple entre \(H-Csp^3-Csp^3-H\)
\(\mathsf{V=\mbox{1,50 kcal.mol}^{-1} \quad n = 3 \quad \mbox{et}\quad\Phi_0=0°}\)
Exemple :
- Cas d'une liaison simple entre deux H-Csp2-Csp2-H
\(\mathsf{V=\mbox{30,0 kcal.mol}^{-1} \quad n = 2 \quad \mbox{et}\quad\Phi_0}=180°\)
Remarque :
Pour certains types de liaisons, on doit faire intervenir plusieurs termes ayant des périodicités différentes.
Par exemple pour la torsion autour de la liaison amide H-N-Csp2, on fait intervenir un terme de périodicité \(\mathsf{n = 2 \quad \mbox{et}\quad \Phi_0}=180°\), du à l'hybridation sp2, et un terme de périodicité \(\mathsf{n = 0 \quad \mbox{et}\quad \Phi_0}=0°\),du à la position relative des atomes d'hydrogène et d'oxygène.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Remarque :
L'énergie totale de la barrière de rotation autour d'une liaison est la somme de tous les termes énergétiques qui varient au cours de la rotation. C'est-à-dire non seulement l'énergie de torsion, mais aussi les termes énergétiques entre atomes non liés dont la position respective change au cours de la rotation : énergie de van der Waals, énergie d'interaction électrostatique.
Considérons le cas de la rotation autour de la liaison centrale du butane.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Lors de la rotation autour de la liaison centrale, la distance entre les deux atomes de carbone en 1 et 4 varie; elle passe de 3,88 \(\mathring{\textrm{A}}\) pour \(\mathsf{\Phi}=180°\) (trans) à 2,57 \(\mathring{\textrm{A}}\) pour \(\mathsf{\Phi}=0°\) (cis).
Pour les atomes d'hydrogènes les plus proches portés par les groupes méthyles, la distance passe de 4,34 \(\mathring{\textrm{A}}\) pour la conformation trans à 1,84 \(\mathring{\textrm{A}}\) pour la conformation cis. Il en résulte que les termes d'énergie d'interaction entre atomes non liés - énergie d'interaction électrostatique (voir paragraphe 2.1) et énergie de van der Waals (voir paragraphe 2.2) – qui dépendent fortement des distances entre atomes non liés vont varier avec l'angle de torsion \(\mathsf{\Phi}\).
L'énergie de torsion \(E_{Torsion}\) devra donc être paramétrée de telle sorte que la somme de tous les termes énergétiques du champ de force reproduise correctement la variation d'énergie potentielle totale en fonction de l'angle de torsion.
Exemple :
Par exemple dans le champ de force Amber, l'énergie de torsion fait intervenir trois termes :
\(V1=\mbox{0,18 kcal.mo}l^{-1} \quad n_1 =3 \quad \mbox{et}\quad \mathsf{\Phi_{0,1}=0°}\)
\(V2=\mbox{0,25 kcal.mo}l^{-1} \quad n_2 =2 \quad \mbox{et}\quad\mathsf{\Phi_{0,2}=180°}\)
\(V3=\mbox{0,18 kcal.mo}l^{-1} \quad n_3 =3 \quad \mbox{et}\quad\mathsf{\Phi_{0,3}=180°}\)
Ces courbes ainsi que leur somme sont représentées dans la figure suivante :
Si on ajoute les termes d'interactions électrostatiques, calculés selon la relation :
\(E_{Electrostatique} = \displaystyle{\sum_{i = 1}^{N - 1} {\sum_{j = i + 1}^N {\frac{{q_i q_j }}{{4\pi \epsilon r_{i,j} }}}}}\) (voir paragraphe 2.2)
\(qi \; \mbox{et} \; qj\) sont les charges ponctuelles portées par les atomes i et j.
\(r_{i,j}\) est la distance entre les atomes i et j.
\(\epsilon\) est la permittivité du milieu.
et de van der Waals, calculés selon la relation :
\(E_{van \; der \;Waals} = \displaystyle{\sum_{i = 1}^{N - 1} {\sum_{j = i + 1}^N {\left[ {\frac{{A_{i,j} }}{{r_{i,j}^{12} }} - \frac{{B_{i,j} }}{{r_{i,j}^6 }}} \right]}}}\)
\(r_{i,j}\) est la distance entre les atomes i et j.
\(A_{i,j} \; \mbox{et} \; B_{i,j}\) sont des paramètres du champ de force qui dépendent du type des atomes i et j
On obtient la courbe suivante :
