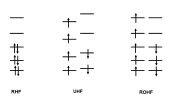Les différentes méthodes de chimie computationnelle

Nous avons vu dans le chapitre précédent, dans le développement de la méthode Hartree-Fock, qu'on est amené à calculer un grand nombre d'intégrale de la forme :

étant donné que les intégrales J et K sont développées sur les Orbitales Atomiques du système.

Les méthodes semi-empiriques

Dans le développement de la méthode Hartree-Fock présenté dans le chapitre précédent, toutes ces intégrales sont calculées, y compris celles impliquant les électrons internes.

Dans les méthodes semi-empiriques, ce protocole de calcul va être simplifié en appliquant diverses approximations supplémentaires :

• la contribution des électrons internes sera négligé

• les électrons de valence seront représentés par une base minimale de Slater (voir chapitre précédent)

• certaines intégrales seront évaluées à l'aide de paramètres empiriques

• la plupart des intégrales multicentriques seront négligées.

Il existe ainsi de nombreuses méthodes semi-empiriques qui dépendent du nombre de simplifications (types d'interactions négligées) et des paramétrages : CNDO, NNDO, MNDO, AM1, PM3, SAM1.

La méthode AM1, développée en 1985, est la plus utilisée et donne souvent de très bons résultats pour un temps de calcul très réduit par rapport aux méthodes ab initio. Dernièrement, ces méthodes commencent à introduire un traitement des électrons d : méthodes AM1/d, PM3/d...

Les méthodes Hartree-Fock restreintes (RHF et ROHF) et la méthode non-restreinte (UHF)

Dans un nombre important de systèmes moléculaires, les niveaux énergétiques sont occupés par deux électrons de spin opposés. Dans chacune de ces couches électroniques, chaque électron est soumis à la répulsion des paires d'électrons des autres niveaux et aussi à la répulsion du deuxième électron de la couche considérée qui est en spin opposé. Dans le cadre de la méthode RHF, on attribue à ces deux électrons la même contribution, donc les mêmes coefficients. Le schéma ci-dessous présente ce schéma :

Certains systèmes chimiques présentent des électrons célibataires sur leur couche externe, il s'agit de systèmes radicalaires. Dans ce cadre, les électrons a et b ne sont pas soumis aux mêmes répulsions de la part des électrons des autres couches car ils n'interagissent pas avec le même nombre d'électrons de chaque spin. Dans le cadre de l'approximation LCAO, leurs coefficients seront donc définis indépendamment lors du processus SCF. Ce protocole mène à la définition de spinorbitales a et b , décrivant le même état, n'ayant pas la même énergie. Cette méthode est dénommée UHF (Unrestricted Hartree-Fock).

Un des corollaires à cette méthode est que les électrons a et b d'un même niveau ne partagent pas nécessairement la même fonction d'espace et bien que l'énergie totale s'en trouve améliorée, il est possible que la fonction d'onde ne soit plus une fonction propre de l'opérateur S². Cet inconvénient peut-être évité si l'on impose une égalité des coefficients pour les spinorbitales a et b de toutes les Orbitales Moléculaires . Cette méthode s'appelle ROHF (Restricted Open Shell Hartree Fock).