Lois expérimentales
Figure de diffraction obtenue sur un cristal d'argent (poudre) avec des rayons X de longueur d'onde 0,71 Angström

Figure de diffraction obtenue sur un cristal d'argent (poudre) avec des électrons d'énergie 362 eV

L'analogie entre les clichés de diffraction des électrons et des rayons X conduit à utiliser le même type de loi descriptive, c'est-à-dire celle de la diffraction des rayons X par les atomes d'un cristal.
La diffraction est essentiellement un phénomène ondulatoire et la formule classique de la diffraction des rayons X par un réseau cristallin s'écrit :
\(\mathbf{2.d.\sin\theta=n.\lambda}\)
C'est la loi de Bragg.
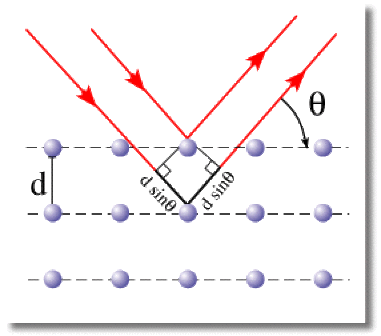
Dans cette formule, \(\textrm d\) représente la distance entre deux plans d'atomes du cristal, \(\theta\) est l'angle d'incidence du faisceau par rapport au plan d'atomes qui conduit à l'apparition de taches de diffraction, \(\lambda\) est la longueur d'onde du rayonnement incident et \(\textrm n\) est un entier.
Connaissant les distances \(\textrm d\) caractéristiques du cristal et les angles de diffraction des électrons, on peut alors déterminer une longueur d'onde \(\lambda_\textrm{exp}\) caractéristique du phénomène de diffraction électronique.
L'intensité du courant collecté présente aussi la même variation avec l'angle de diffraction que l'intensité diffractée d'un rayonnement X de même longueur d'onde.
Le tableau ci-dessous rassemble quelques valeurs expérimentales obtenues en faisant varier la tension accélératrice \(\mathrm{V_a}\).
\(\mathrm{V_a}\) (Volts) | 10190 | 11150 | 13480 |
\(\lambda_{\exp}\) (mètre) | 1.21 10-11 | 1.15 10-11 | 1.05 10-11 |
\(\lambda_{\exp}\sqrt{\mathrm{V_a}}\) | 12.22 10-10 | 12.15 10-10 | 12.20 10-10 |
On constate expérimentalement qu'il existe une relation liant les caractéristiques corpusculaires de l'électron (masse et quantité de mouvement) et le phénomène ondulatoire:
\(\mathbf{\lambda_\textrm{exp}\sqrt{\mathrm{V_a}}=\frac{\lambda_\textrm{exp}.p}{\sqrt{2.\textrm m_\textrm e.\textrm e}}=\textrm{constante}}\)
De plus, l'effet observé subsiste, même lorsque la densité des électrons est si faible qu'ils passent dans l'appareil un à un. Le comportement ondulatoire est donc une caractéristique intrinsèque de la particule.