Introduction
Le plan \(P\) est orienté. Soit \(C\) le cercle de centre \(O\) et de rayon \(1,\) orienté dans le sens direct et muni d'un point origine \(I.\)
On admet qu'il existe une bijection \(\psi\) de l'intervalle \([0, 2\pi[\)sur le cercle \(C.\) Cette bijection associe à tout réel \(y~\textrm{de}~[0, 2\pi[\)le point \(M~\textrm{de}~C\) tel que la longueur de l'arc \(IM\) parcouru dans le sens direct soit égale à \(y.\)
\(\mathbb R\) est archimédien, donc pour tout réel \(x\) il existe un unique entier relatif \(k\) tel que \(k(2\pi) \leq x < (k+1)(2\pi).\)
Soit \(y = x - 2k\pi,\) alors \(y \in [0, 2\pi[~\textrm{et}~x-y \in 2\pi \mathbb Z.\)
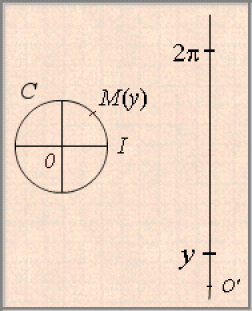
Pour tout réel \(x\) il existe donc un réel \(y\) appartenant à l'intervalle \([0, 2\pi[\)tel que \(x-y\)appartient à \(2\pi\mathbb Z.\) Ce réel \(y\) est unique.
A tout réel \(x\) on peut donc associer un point unique \(M~\textrm{de}~C,\) \(M\) étant l'image du réel \(y\) par la bijection \(\psi.\) Il existe donc une surjection \(\rho~\textrm{de}~\mathbb R~\textrm{sur}~\mathbb C.\)
Si le point \(M\) est l'image du réel \(x\) par \(\rho,\) l'ensemble des antécédents de \(M\) par\(\rho\) est l'ensemble des réels de la forme \(x + 2k\pi,~k \in \mathbb Z.\)