Fonction exponentielle
Théorème - définition
La fonction logarithme népérien est continue et strictement croissante sur \(]0, +\infty[\) et \(\ln(]0, +\infty[) = \mathbb R.\) On peut donc lui appliquer le théorème des fonctions réciproques qui conduit au théorème suivant.
Théorème : définition de la fonction exponentielle
La fonction logarithme népérien admet une fonction réciproque définie sur \(\mathbb R\) qui établit une bijection entre \(\mathbb R\) et \(]0, +\infty[.\) Cette fonction, appelée fonction exponentielle, est notée \(x \mapsto \exp x.\)
On a donc : \(\boxed{y = \exp x,~~x \in \mathbb R} \Leftrightarrow \boxed{x = \ln y,~~y \in ]0, +\infty[}\)
Propriétés et formulaire
En appliquant le théorème des fonctions continues, strictement monotones et dérivables sur un intervalle de \(\mathbb R,\) on obtient :
La fonction exponentielle est continue, strictement croissante et dérivable sur \(\mathbb R\) :
\(\displaystyle \lim_{x \rightarrow - \infty}\exp x = 0,\) \(\exp 0 = 1,\) \(\displaystyle \lim_{x \rightarrow +\infty} \exp x = +\infty,\) \(\exp' x = \exp x\)
En effet :
\(\forall x \in \mathbb R~~y = \exp x \Leftrightarrow x = \ln y,~~\ln' y = \frac{1}{y},~~\ln' y \neq 0,~~\exp' x = \frac{1}{\ln' y} = y = \exp x\)
De plus elle vérifie la relation :\(\forall (a, b) \in \mathbb R^2~~\exp(a+b) = (\exp a)(\exp b)\) .
Car \(\ln(\exp(a+b)) = a + b = \ln(\exp a) + \ln(\exp b),\)
or \(\ln(\exp a) + \ln(\exp b) = \ln((\exp a)(\exp b)),\)
donc \(\ln(\exp(a+b)) = \ln((\exp a)(\exp b)),\) ce qui termine la démonstration en utilisant l'injectivité du logarithme népérien.
On peut alors regrouper les propriétés de la fonction exponentielle
Propriété :
La fonction exponentielle est une fonction définie sur \(\mathbb R,\) dérivable, telle que \(\forall x \in \mathbb R~~\exp' x = \exp x,~~\exp 0 = 1.\)
Elle vérifie \(\forall (a,b) \in \mathbb R^2~~\exp(a+b) = (\exp a)(\exp b).\)
En outre elle est strictement croissante et a pour image l'intervalle \(]0, +\infty[.\)
Comme pour la fonction logarithme on a un formulaire
\(\boxed{\forall (a, b) \in \mathbb R^2,~~\forall n \in \mathbb N^*}\\ \boxed{\exp(a+b) = (\exp a)(\exp b)~~(1)~~}\boxed{\exp(na) = (\exp a)^n~~(2)}\\ \boxed{\exp(a-b) = \frac{\exp a}{\exp b}~~(3)~~~~~~~~~~~~~~~}\boxed{\exp(-b) = \frac{1}{\exp b}~~(4)~~~}\)
Démonstration :
\((1)\) déjà fait,
\((2)\) par récurrence,
\((3)\) \(\begin{cases} \ln(\exp(a-b)) = a-b = \ln(\exp a) - \ln(\exp b) = \ln(\frac{\exp a}{\exp b}) \\ \Rightarrow \exp(a-b) = \frac{\exp a}{\exp b}\end{cases}\)
\((4)\) appliquer la relation précédente au cas \(a = 0.\)
Propriété :
\(\displaystyle \lim_{x \rightarrow +\infty}\frac{\exp x}{x} = +\infty\)
Démonstration :
\(\forall x > 0~~\frac{\exp x}{x} = \frac{\exp x}{\ln(\exp x)} = \frac{y}{\ln y}\)or\(\displaystyle \lim_{x \rightarrow +\infty} \exp x = +\infty,\) \(\displaystyle \lim_{y \rightarrow +\infty}\frac{\ln y}{y} = 0\)
ceci termine la démonstration.
Représentation graphique
\(\begin{array}{|c | c c c|}\hline x & -\infty & & +\infty \\ \hline & & & +\infty \\ \exp x & & \nearrow & \\ & 0 & & \\ \hline \end{array}\)
\(\color{blue} x \mapsto \exp x\)
\(\color{red} x \mapsto \ln x\)
\(\color{green} x \mapsto x\)
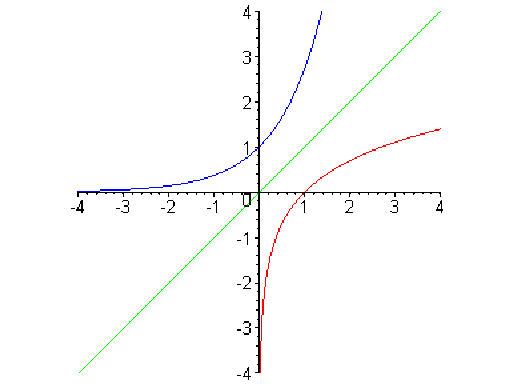
Le graphe de l'exponentielle est symétrique du graphe du logarithme par rapport à la première bissectrice.
On observe sur le graphe de l'exponentielle que :
la droite d'équation \(y = 0\)est une asymptote,
le graphe présente une branche parabolique de direction verticale car \(\displaystyle \lim_{x \rightarrow +\infty}\frac{(\exp x)}{x} = +\infty.\)
Remarque :
Il est possible d'effectuer une autre démarche pour introduire les fonctions exponentielle et logarithme népérien.