Produit de matrices de passage
Soient\( \mathcal B, \mathcal B'\) et \(\mathcal B''\) trois bases de l'espace vectoriel \(E\). On a le schéma :
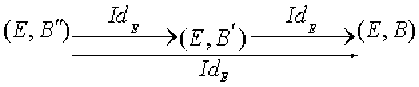
Il permet d'écrire l'égalité :
\([\mathcal Id_E]_{\mathcal B"}^{\mathcal B}=[\mathcal Id_E]_{\mathcal B'}^{\mathcal B}[\mathcal Id_E]_{\mathcal B"}^{\mathcal B'}\)
D'où la propriété des matrices de passage :
Proposition :
Soient\( \mathcal B, \mathcal B'\) et \(\mathcal B"\) trois bases d'un espace vectoriel de type fini \(E\). Alors
\(\mathcal P_{\mathcal B,\mathcal B"}=\mathcal P_{\mathcal B,\mathcal B'}\mathcal P_{\mathcal B',\mathcal B"}\)