Définition
Ce paragraphe suppose connue la notion de matrice de passage entre deux bases et son interprétation comme matrice associée à l'application identique par rapport à des bases bien choisies.
Matrice de changement de base
Soient \(B\) et \(B'\) deux bases d'un espace vectoriel de dimension \(n\).
Définition :
On appelle matrice de passage de la base \(B\) à la base \(B'\) la matrice carrée d'ordre \(n\) dont la \(j\)-ième colonne est formée des coordonnées du \(j\)-ième vecteur de la base \(B'\), par rapport à la base \(B\).
On note \(P_{B,B'}\) la matrice de passage de la base \(B\) à la base \(B'\)
Cette matrice peut être interprétée comme la matrice associée à l'application identique de \(E\) par rapport à des bases bien choisies.
On sait qu'en prenant sur l'espace de départ et sur l'espace d'arrivée la même base, la matrice associée à l'application identique est la matrice \(I_n\).
Par contre ce n'est pas le cas si les bases sur \(E\) espace de départ et \(E\) espace d'arrivée sont différentes.
Soient donc \(B=(e_1,e_2,\ldots,e_n)\) et \(B'=(e'_1,e'_2,\ldots,e'_n)\) deux bases différentes de \(E\).
D'après la définition de la matrice de passage de \(B\) à \(B'\), la \(j\)-ième colonne de \(P_{B,B'}\) est formée des coordonnées du vecteur \(e'_j\) sur la base \(B=(e_1,e_2,\ldots,e_n)\).
Il est donc nécessaire, pour que cette matrice soit celle de l'identité, que la base de l'espace de départ soit \(B'\) et celle de l'espace d'arrivée \(B\) puisque le vecteur
\(e'_j=Id_E(e'_j)\) est exprimé sur \(B\).
On est donc amené à considérer le schéma suivant :
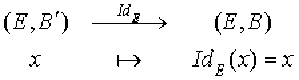
Alors si \(B=(e_1,e_2,\ldots,e_n)\) et \(B'=(e'_1,e'_2,\ldots,e'_n)\), on a \(Id_E(e'_j)=e'_j=\displaystyle{\sum^n_{i=1}}a_{i,j}e_i\) et \(\textrm{Mat}^{B}_{B'}(Id_E)\) est la matrice dont la \(j\)-ième colonne est formée des composantes de \(e'_j\) par rapport à \(B=(e_1,e_2,\ldots,e_n)\), soit \(\begin{array}{c}a_{1,j}\\a_{2,j}\\\vdots\\a_{n,j}\end{array}\).
Cette colonne est la \(j\)-ième colonne de \(P_{B,B'}\). On a donc le résultat suivant
Propriété : Interprétation de la matrice de passage à l'aide de l'application identique
Soient \(B\) et \(B'\) deux bases de \(E\). La matrice de passage de \(B\) à \(B'\) est égale à la matrice de l'application identique de \(E\), avec \(B'\) comme base de l'espace de départ et \(B\) comme base de l'espace d'arrivée.
\(P_{B,B'}=\textrm{Mat}^{B}_{B'}(id_E)\)
Attention :
à l'ordre des bases dans cette formule.
Matrice inverse d'une matrice de passage
Comme l'application identique est un automorphisme, sa matrice \(\textrm{Mat}^{B}_{B'}(Id_E)\) est inversible et donc aussi \(P_{B,B'}\).
On sait, que \(\left[\textrm{Mat}^{B}_{B'}(Id_E)\right]^{-1}=\textrm{Mat}^{B}_{B'}(Id_E^{-1})=\textrm{Mat}^{B}_{B'}(Id_E)\) puisque l'identité est égale à sa propre application réciproque.
Attention aux places des bases dans ces égalités
Or, d'après la définition de la matrice de passage d'une base à une autre, \(\textrm{Mat}^{B}_{B'}(Id_E)\) est la matrice de passage de la base \(B'\) à la base \(B\). On a donc la propriété suivante :
\(\left[P_{B,B'}\right]^{-1}=P_{B',B}\)
Produit de matrice de passage avec un bon choix de bases
Soient \(B\), \(B'\) et \(B''\) trois bases de \(E\).
On a la relation \(\textrm{Mat}^{B}_{B''}(Id_E)=\textrm{Mat}^{B}_{B''}(Id_E)\textrm{Mat}^{B}_{B'}(Id_E)\).
D'où \(P_{B,B''}=P_{B',B''}P_{B,B'}\).
Autres définitions et propriétés
Soit \(E\) un espace vectoriel réel de dimension \(n\). Soient \(B=(e_1,e_2,\ldots,e_n)\) et \(B'=(e'_1,e'_2,\ldots,e'_n)\) deux bases de \(E\).
Comme \(B'\) est une base de \(E\), ses vecteurs sont linéairement indépendants et \(\det_B(\epsilon_1,\epsilon_2,\ldots,\epsilon_n)\) est non nul. De plus, l'espace vectoriel considéré étant réel, \(\det_B(\epsilon_1,\epsilon_2,\ldots,\epsilon_n)\) est un nombre réel, non nul, et il a un signe.
Ces remarques permettent de définir une relation binaire sur les bases de \(E\).
Définition :
Si \(B=(e_1,e_2,\ldots,e_n)\) et \(B'=(\epsilon_1,\epsilon_2,\ldots,\epsilon_n)\) sont deux bases de \(E\), on dit que \(B'\) a même sens que \(B\) si :
\(\det_B(\epsilon_1,\epsilon_2,\ldots,\epsilon_n)>0\)
Remarque :
Il est immédiat, compte tenu de cette définition et des propriétés qui suivent, que tout les résultats qui vont être obtenus ne sont valables que pour un espace vectoriel réel puisque ils font intervenir avec force la relation d'ordre sur \(R\) et le fait que \(R\) est un corps totalement ordonné
Pour faciliter ici l'expression, on utilise la notation \(B\Re B'\Leftrightarrow\det_B(B')>0\) en notant \(\det_B(B')=\det_B(\epsilon_1,\epsilon_2,\ldots,\epsilon_n)\).
Propriété : de cette relation
elle est réflexive c'est-à-dire que pour toute base \(B\) de \(E\), \(B\) a même sens que \(B\), soit :
\(B\Re B\)
Cela est immédiat puisque \(\det_B(B)=1\).
elle est symétrique c'est-à-dire que pour toutes bases \(B\) et \(B'\) de \(E\), si \(B'\) a même sens que \(B\), alors \(B\) a même sens que \(B'\), soit :
\(B\Re B'\Rightarrow B'\Re B\)
Pour le démontrer, on va faire intervenir la matrice de passage de la base \(B\) à la base \(B'\). C'est la matrice, notée \(P_{B,B'}\), dont la \(j\)-ième colonne est formée des coordonnées du \(j\)-ième vecteur de la base \(B'\), par rapport à la base \(B\).
Cela permet d'interpréter le déterminant de la base \(B'\) par rapport à la base \(B\) comme le déterminant de la matrice de passage de \(B\) à \(B'\).
De plus on sait que \(\left[P_{B,B'}\right]^{-1}=P_{B',B}\). Donc le déterminant de la base \(B\) par rapport à la base \(B'\) est le déterminant de la matrice de passage de \(B'\) à \(B\) d'où les relations :
\(\det_B(B')=\det(P_{B,B'})\) et \(\det_{B'}(B)=\det(\left[P_{B,B'}\right]^{-1})\)
L'égalité \(P_{B,B'}P_{B',B}=I_n\) implique alors : \(\det(P_{B,B'})\det(P_{B',B})=1\) et donc \(\det_B(B')\det_{B'}(B)=1\).
Ces déterminants sont donc de même signe, ce qui achève la démonstration.
elle est transitive c'est-à-dire que si \(B\), \(B'\) et \(B''\) sont trois bases de \(E\), si \(B'\) a même sens que \(B\) et \(B''\) même sens que \(B'\), alors \(B''\) a même sens que \(B\), soit :
\(B\Re B'\) et \(B'\Re B''\Rightarrow B\Re B''\)
C'est encore une propriété des matrices de passage d'une base à une autre qui va servir, plus précisément la formule \(P_{B,B''}=P_{B',B''}P_{B,B'}\) où \(B\), \(B'\) et \(B''\) sont trois bases de \(E\).
Il résulte en effet de cette relation et des propriétés des déterminants, que \(\det(P_{B,B''})=\det(P_{B',B''})\det(P_{B,B'})\) et donc \(\det_B(B'')=\det_B'(B'')\det_B(B')\).
Donc si les deux réels du second membre de cette égalité sont positifs, celui du membre de gauche l'est aussi, ce qui achève la démonstration.
Définition : (pour les étudiants qui ne connaîtraient pas déjà cette notion)
Une relation binaire vérifiant ces trois propriétés réflexivité, symétrie et transitivité est appelée relation d'équivalence.
Théorème : Définition
Soit \(E\) un espace vectoriel réel de type fini.
La relation binaire définie sur l'ensemble des bases de \(E\) par :
\(B\) et \(B'\) étant des bases de E, \(B\Re B' \Leftrightarrow \det_B(B')>0\)
est une relation d'équivalence.
Si \(B\Re B'\) on dit aussi que \(B\) et \(B'\) ont même orientation.
La question qui se pose alors est la suivante : une base \(B_0\) étant choisie sur \(E\), combien y a-t-il d'orientation possible sur \(E\) ?
Comme \(R\) est totalement ordonné, si \(B\) est une base quelconque de \(E\), il n'y a que deux possibilités pour le réel \(\det_{B_0}(B)\):
ou bien il est strictement positif (\(B\) et \(B_0\)ont même orientation),
ou bien il est strictement négatif (on dit que \(B\) a une orientation opposée à celle de \(B_0\)).
En effet il ne peut être nul puisque \(B\) étant une base de \(E\), ses vecteurs sont linéairement indépendants et par conséquent leur déterminant par rapport à une base est non nul (propriété des déterminants).
On peut donc ranger les bases de \(E\) en deux classes (pour ceux qui connaissent ce vocabulaire, ce sont les classes d'équivalence de la relation \(\Re\)).
La classe des bases qui ont même orientation que \(B_0\) (par exemple la base \(B_0\) elle-même).
La classe des bases qui ont une orientation contraire à celle de \(E_0\) (par exemple si \(B_0=(b_1,b_2,\ldots,b_n)\), la base \(B'_0=(-b_1,b_2,\ldots,b_n)\)).
Définition : Orientation de E
Choisir une de ces deux classes, c'est par définition orienter le \(R\)-espace vectoriel \(E\). Il y a donc deux orientations possibles.
Les bases appartenant à la classe choisie sont appelées directes ou positivement orientées, les bases appartenant à l'autre classe sont appelées indirectes ou rétrogrades ou négativement orientées.
Remarque :
Pour orienter l'espace en général, on prend une base et on choisit la classe la contenant ; autrement dit on qualifie de directe les bases qui ont même orientation que la base choisie.
La notion d'orientation n'est pas intrinsèque et est de plus assez arbitraire car il n'y a pas forcément de choix naturel de base de référence.
Par contre, dans \(R^n\), il est naturel de définir l'orientation à partir de la base canonique et de choisir comme orientation la classe la contenant ; dans ce cas la base canonique est directe.