Allure locale d'une branche infinie
On considère \(f :]\alpha, \beta[ \rightarrow\mathbb R\), avec \(\beta\in\mathbb R\) ou \(\beta=+\infty\) ; on note toujours \(\Gamma\) le graphe de \(f\) et \(M(x)\) le point de coordonnées \((x , f(x))\).
Remarque :
nous ferons l'étude du comportement de la courbe au voisinage de \(\beta\) ; les notions sont analogues au voisinage de \(\alpha\) ; on se ramène à l'étude en \(\beta\) en changeant \(x\) en \(-x\).
Définition :
On dit que \(\Gamma\) présente une branche infinie en \(\beta\) dans chacun des deux cas suivants :
\(\beta=+\infty\);
ou \(f\) est non bornée au voisinage de \(\beta\)
On a, en particulier, une branche infinie lorsque la distance de l'origine 0 à \(M(x)\) tend vers \(+\infty\) lorsque \(x\) tend vers \(\beta\) ; ce n'est pas toujours le cas, par exemple :
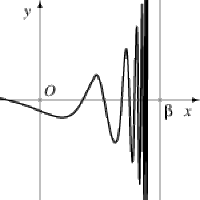
Dans la suite nous envisagerons l'un des cas particuliers :
\(\beta=+\infty\) ou \(\lim_{x\rightarrow\beta}f(x)=+\infty\) ou \(\lim_{x\rightarrow\beta}f(x)=-\infty\)
Les deux situations suivantes sont bien connues
\(\beta=+\infty\) et \(\lim_{x\rightarrow+\infty}f(x)=l\in\mathbb R\) : la droite d'équation \(y=l\) est asymptote horizontale ;
\(\beta\in\mathbb R\) et \(\lim_{x\rightarrow\beta}f(x)=+\infty\) ou \(\lim_{x\rightarrow\beta}f(x)=-\infty\) ; la droite \(y=\beta\) est asymptote verticale.