Exercice n°3
Partie
Question
On considère la relation :
\(\displaystyle{\frac{1}{1-t}=1+t+t^2+t^3+t^4+t^4\epsilon(t)}\)
avec \(\epsilon(t)\) tendant vers \(0\) quand \(t\) tend vers \(0\)
\(\displaystyle{\frac{1}{x-1}=\frac{1}{x}\left(1+\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x^3}+\frac{1}{x^4}+\frac{1}{x^4}\epsilon\left(\frac{1}{x}\right)\right)}\)
avec \(\displaystyle{\epsilon\left(\frac{1}{x}\right)}\) tendant vers \(0\) quand \(x\) tend vers \(\infty\). En déduire la forme du graphe des fonctions :
\(\displaystyle{h_1 : x\rightarrow\frac{x^2}{x-1}}\)
\(\displaystyle{h_2 : x\rightarrow\frac{x^4}{x^2-1}}\)
\(\displaystyle{h_3 : x\rightarrow\frac{x^5}{x^4-1}}\)
\(\displaystyle{h_4 : x\rightarrow\frac{x^3}{x-1}}\)
\(\displaystyle{h_5 : x\rightarrow\frac{x^2}{x^4-1}}\)
\(\displaystyle{h_6 : x\rightarrow\frac{x^2}{x^3-1}}\)
Rappel de cours
Voyons comment les développements limités permettent de préciser l'allure locale du graphe d'une fonction, en particulier en donnant une tangente, et la position du graphe par rapport à cette tangente.
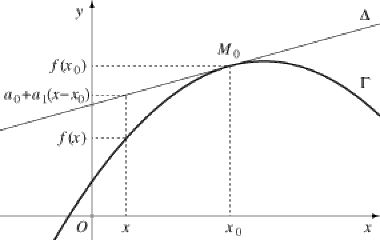
Considérons une fonction \(f\) définie au voisinage d'un \(x_0\in\mathbb R\). On a vu qu'il est équivalent de dire que \(f\) (ou son prolongement en \(x_0\)) est dérivable en \(x_0\) ou de dire que \(f\) admet un développement limité à l'ordre 1 (au moins). Nous supposerons cette condition réalisée, et nous noterons \(a_0=f(x_0)\) et \(a_1=f'(x_0)\).
On sait que le graphe \(\Gamma\) de \(f\) admet alors une tangente \(\Delta\) en \(x_0\), d'équation \(y=a_0+a_1(x-x_0)\).
Supposons de plus qu'il existe un entier \(p\ge2\) tel que \(f\) admette un développement limité à l'ordre \(p\), de la forme
f(x)=a_0+a_1(x-x_0)+a_p(x-x_0)^p+(x-x_0)^p\epsilon(x) avec \(a_p\ne0\),
c'est-à-dire que tous les cœfficients \(a_k\) sont nuls pour \(1<k<p\), et \(a_p\) non nul ; on dit que c'est le premier développement limité significatif de \(f\).
Alors le signe de \(a_p\) donne la position de \(\Gamma\) par rapport à la droite \(\Delta\).
Pour le voir, il suffit d'écrire le développement limité précédent sous la forme
\(f(x)-y=(x-x_0)^p(a_p+\epsilon(x))\).
Vu que \(\displaystyle{\lim_{x\rightarrow x_0}\epsilon(x)=0}\), le signe de la parenthèse \((a_p+\epsilon(x))\) est au voisinage de \(x_0\) le même que celui de \(a_p\) (il suffit d'utiliser la définition de la limite).
D'autre part, le signe de \((x - x_0)^p\) est :
positif si \(p\) est pair ;
positif pour \(x>x_0\) et négatif pour \(x<x_0\) si \(p\) est impair.
Ainsi, on connaît localement le signe de \(f(x)-y\), c'est-à-dire la position locale du graphe de \(f\) par rapport à la tangente \(\Delta\) :
quand \(f(x)-y>0\), \(\Gamma\) est au dessus de \(\Delta\);
quand \(f(x)-y<0\), \(\Gamma\) est au dessous de \(\Delta\).
Solution détaillée
Quand \(x\) tend vers l'infini, on peut écrire ces fonctions de la façons suivante :
\(\displaystyle{h_1(x)=x+1+\frac{1}{x}+\frac{1}{x}\epsilon_1\left(\frac{1}{x}\right)}\)
\(\displaystyle{h_2(x)=x^2+x+1+\frac{1}{x}\epsilon_2\left(\frac{1}{x}\right)}\)
\(\displaystyle{h_3(x)=x+1+\frac{1}{x}+\frac{1}{x}\epsilon_3\left(\frac{1}{x}\right)}\)
\(\displaystyle{h_4(x)=x^2+x+1+\frac{1}{x}\epsilon_4\left(\frac{1}{x}\right)}\)
\(\displaystyle{h_5(x)=\epsilon_5\left(\frac{1}{x}\right)}\)
\(\displaystyle{h_6(x)=\epsilon_6\left(\frac{1}{x}\right)}\)
où \(\displaystyle{\epsilon\left(\frac{1}{x}\right)}\) tendant vers \(0\) quand \(x\) tend vers \(\infty\).

\(h_1(x)\) et \(h_3(x)\) ont la même forme et sont proches de la droite \(y=x+1\).

\(h_2(x)\) et \(h_4(x)\) ont la même forme et sont proches de la parabole \(y=x^2+x+1\).

\(h_5(x)\) et \(h_6(x)\) sont asymptotes à l'axe des \(x\).