Exercice n°1
Partie
Soient \(a< b\) deux réels, et \(f\) une fonction continûment dérivable vérifiant :
\(f(a)=f(b)=0\) et \(f(y)>0\) si \(a< y< b\).
Nous allons étudier quelques propriétés des solutions de l'équation autonome \(y'=f(y)\).
Question
Trouver deux solutions constantes.
Solution détaillée
L'équation \(y'=f(y)\) est autonome, puisque la variable \(x\) n'intervient pas dans l'équation.
Les fonctions constantes \(y_1=a\) et \(y_2=b\) sont solutions : en effet, puisque \(f(a)=f(b)=0\), on a
\(y'_i(x)=0=f(y_i)\) pour \(i=1\).
Question
Soit \(u(x)\) une solution vérifiant \(a< u(0)< b\). Montrer qu'on a, pour tout \(x\) où \(u\) est définie, \(a< u(x)< b\). En déduire que \(u\) est définie sur \(\mathbb R\) tout entier, et croissante.
Deux graphes de solutions ne se rencontrent pas.
Solution détaillée
Puisque \(f\) est continûment dérivable, on peut appliquer le théorème d'existence et d'unicité.
Soit \(u\) une solution vérifiant \(a< u(0)< b\). Le graphe de \(u\) ne peut pas croiser les graphes de \(y_1\) et \(y_2\), à savoir les horizontales \(y=a\) et \(y=b\). On a donc, pour tout \(x\), \(a< u(x)< b\). La fonction \(u\) n'a pas d'asymptote verticale et est donc définie sur \(\mathbb R\) tout entier (voir théorème de prolongement dans le chapitre Existence et unicité).
D'autre part, pour tout \(x\), on a \(u'(x)=f(u(x))\). Puisque \(f(y)>0\) si \(a< y< b\), \(u'(x)>0\), donc \(f\) est croissante sur \(\mathbb R\).
Question
Montrer que, quand \(x\) tend vers \(+\infty\), \(u(x)\) tend vers une limite \(l\), inférieure ou égale à \(b\), et que \(u'\) tend vers \(f(l)\).
Si\(f\) est une fonction définie sur \(R\) croissante et majorée, alors \(f(x)\) tend vers une limite finie quant \(x\) tend vers \(+\infty\).
Solution détaillée
La fonction \(u(x)\), étant croissante et majorée par \(b\), possède une limite \(l< b\) quand \(x\) tend vers \(+\infty\).
Puisque \(f\) est continue, la dérivée \(u'(x)=f(u(x))\) tend vers \(f(l)\) quand \(x\) tend vers \(+\infty\).
Question
Montrer que \(f(l)\ge q0\), puis que \(f(l)=0\) (on pourra raisonner par l'absurde). En déduire que \(l=b\), et que le graphe de \(u\) est asymptote à la droite \(y=b\).
Montrer que si \(f'(x)\) tendait vers un nombre \(m\) strictement positif quand \(x\) tend vers l'infini, alors \(f\) ne serait pas majorée.
Solution détaillée
Puisque \(a<< b\), on a \(f(l)\ge q0\).
Pour montrer que \(f(l)=0\), raisonnons par l'absurde et supposons \(f(l)=a>0\).
Quand \(x\) tend vers \(+\infty\), \(u'(x)\) tendrait vers \(a\), donc il existerait \(x_0\) tel que, si \(x> x_0\), \(u'(x)> a/2\).
Mais alors, pour \(x> x_0\), on aurait \(u(x)> u(x_0)+(a/2)(x-x_0)\).
La fonction \(u\) tendrait vers \(+\infty\) avec \(x\), ce qui est en contradiction avec le fait que \(u\) est bornée.
On a donc \(f(l)=0\). Puisque \(a< l\leq\) et que \(f(y)>0\) si \(a< y< b\), on a forcément \(l=b\).
Question
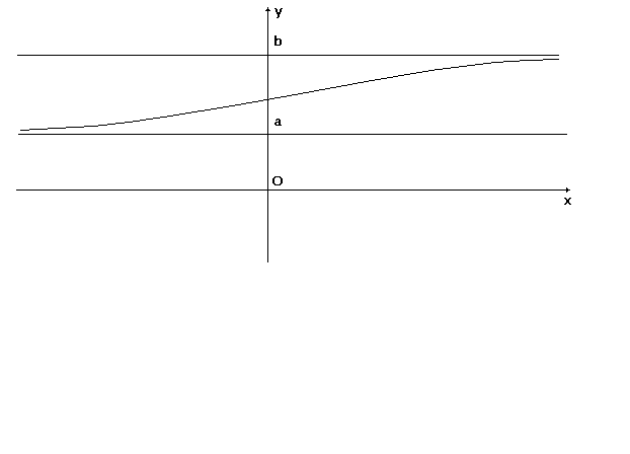
Enoncer les propriétés analogues lorsque \(x\) tend vers \(-\infty\), et tracer le graphe de \(u\).
Solution détaillée
On démontrerait de même que, quand\(x\) tend vers \(-\infty\), \(u'(x)\) tend vers \(0\) et \(u(x)\) tend vers \(a\).
