Problème
Durée : 40 mn
Note maximale : 18
Question
On considère la fonction \(F\) définie par : \(\displaystyle{F(x)=\int_x^{2x}\frac{t^2}{t^2+\sin^2t}dt}\)
Déterminer l’ensemble de définition de la fonction \(F\). Montrer que, pour \(x\) non nul \(F(-x)=-F(x)\) et que \(F\) est prolongeable en une fonction continue en \(0\).
Montrer que la fonction \(F\) ainsi prolongée est de classe \(C^1\) sur \(\mathbb R\) et étudier son sens de variation.
Etudier \(F\) quand \(x\) tend vers \(\pm\infty\).
Tracer approximativement le graphe de \(F\).
Solution
La fonction \(F\) est définie pour tout \(x\ne0\) car alors \(0\) n'appartient pas à l'intervalle d'intégration.
[1 point]
Le changement de variable \(u=-t\) conduit aux égalités :
\(\displaystyle{\forall x\in\mathbb R^*\quad F(-x)=\int_{-x}^{-2x}\frac{t^2}{t^2+\sin^2t}dt=-\int_x^{2x}\frac{u^2}{u^2+\sin^2u}du=-F(x)}\),
la fonction \(F\) est donc impaire.
[1.5 point]
Par ailleurs on a, pour tout \(x\) réel positif, \(\displaystyle{|F(x)|\le\int_x^{2x}dt=x}\) d'où \(\displaystyle{\lim_{x\rightarrow0}F(x)=0}\).
On prolonge \(F\) par continuité en \(0\) en posant \(F(0)=0\) .
[1.5 point]
La fonction \(\displaystyle{x\mapsto\frac{x^2}{x^2+\sin^2x}}\) est continue sur \(]-\infty,0[\) et \(]0,+\infty[\), la fonction \(F\) est donc de classe \(C^1\) sur \(]-\infty,0[\) et \(]0,+\infty[\).
On a, pour tout \(x\) réel non nul : \(\begin{array}{lll}F'(x)&=&\displaystyle{\frac{8x^2}{4x^2+\sin^22x}-\frac{x^2}{x^2+\sin^2x}}\\&=&\displaystyle{\frac{4x^2(x^2+\sin^2x+\sin^4x)}{(4x^2+\sin^22x)(x^2+\sin^2x)}}\\&>&0\end{array}\)
La fonction \(F\) est donc croissante sur \(]0,+\infty[\).
[2 points]
Dérivabilité en 0 :
On étudie quand \(x\) tend vers \(0\) \(~~\displaystyle{\frac{F(x)}{x}=\frac{1}{x}\int_x^{2x}\frac{t^2}{t^2+\sin^2t}dt}\)
soit, pour \(x>0\), d’après la formule de la moyenne : \(\displaystyle{\frac{F(x)}{x}=\frac{\theta^2}{\theta^2+\sin^2\theta}}\) avec \(x<\theta<2x\),
or \(\displaystyle{\frac{\theta^2}{\theta^2+\sin^2\theta}=\frac{1}{1+\frac{\sin^2\theta}{\theta^2}}}\) d'où \(\displaystyle{\lim_{x\rightarrow0}\frac{\theta^2}{\theta^2+\sin^2\theta}=\frac{1}{2}}\)
et \(\displaystyle{\lim_{x\rightarrow0}\frac{F(x)}{x}=\frac{1}{2}}\),
la fonction \(F\) est dérivable en \(0\) et \(\displaystyle{F'(0)=\frac{1}{2}}\).
[4 points]
Or, quand \(x\) tend vers \(0\), on a : \(\displaystyle{F'(x)\sim\frac{8x^4}{16x^4}}\) d'où \(\displaystyle{\lim_{x\rightarrow0}F'(x)=\frac{1}{2}=F'(0)}\).
La fonction \(F’\) est continue en \(0\) et \(F\) est de classe \(C^1\) sur \(\mathbb R\).
[1 point]
Étude au voisinage de \(+\infty\) :
On a, pour tout \(t\) réel positif, \(\displaystyle{\frac{t^2}{t^2+1}\le\frac{t^2}{t^2+\sin^2t}\le1}\) ,
d'où \(\displaystyle{\int_x^{2x}\frac{t^2}{t^2+1}dt\le F(x)\le x}\)
soit \(x-\arctan~2x+\arctan x\le F(x)\le x\)
en divisant les différents termes par \(x\) on voit que \(\displaystyle{\lim_{x\rightarrow+\infty}\frac{F(x)}{x}=1}\).
[3 points]
On étudie alors \(\displaystyle{F(x)-x=\int_x^{2x}\left(\frac{t^2}{t^2+\sin^2t}-1\right)dt=-\int_x^{2x}\frac{\sin^2t}{t^2+\sin^2t}dt}\)
D’où \(\displaystyle{|F(x)-x|\le\int_x^{2x}\frac{\sin^2t}{\sin^2t+t^2}dt\le\int_x^{2x}\frac{1}{t^2}dt=\frac{1}{2x}}\).
[2 points]
On a donc : \(\displaystyle{\lim_{x\rightarrow0}(F(x)-x)=0}\).
le graphe de la fonction \(F\) a donc comme asymptote la droite d'équation \(y=x\) et est en dessous de son asymptote pour \(x>0\).
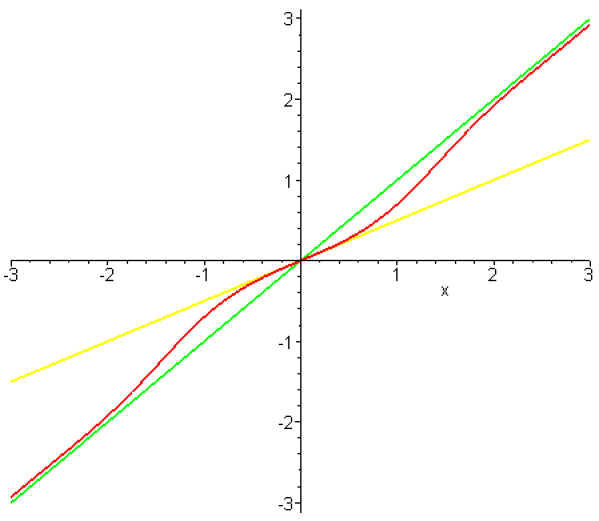
[3 points]