Prévoir la tension issue d'un générateur - Adaptation en tension
Durée : 2 mn
Note maximale : 3
Question
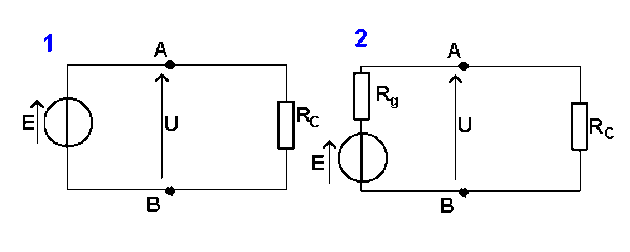
\(E = 12 \mathrm{ V}\), \(R_g = 50 \mathrm{ } \Omega\)
Calculer la tension \(U\) dans le cas du générateur de tension idéal (\(1\)) ou réel (\(2\)) pour \(R_C = 10 \mathrm{ k} \Omega\) et \(R_C = 50 \mathrm{ } \Omega\).
A quelle condition a-t-on \(U \approx E\) \(\forall R_C\) ?
Solution
(1) Le générateur délivre \(E = 12 \mathrm{ V}\) quelle que soit la résistance de charge (1 pt)
(2) Le montage est un diviseur de tension :
\(\displaystyle{ U = E \frac{R_C}{R_g + R_C} = E \frac{1}{1 + \frac{R_g}{R_C}} }\)
Pour \(R_C = 10 \mathrm{ k} \Omega\) : \(U = E = 12 \mathrm{ V}\) ;
Pour \(R_C= 50 \mathrm{ } \Omega\) : \(\displaystyle{ U = \frac{E}{3/2} = \frac{2}{3} E = 8 \mathrm{ V} }\)
Pour que le générateur soit adapté en tension à sa charge \(R_C\), c'est-à-dire \(U \approx E\) \(\forall R_C\), il faut que \(R_g \ll R_C\) (2 pts)