Théorème de Thevenin

Cette transformation permet de remplacer une partie d'un réseau par un générateur de tension[1] qui lui est électriquement équivalent, de manière à simplifier les calculs ultérieurs.

Si, entre deux nœuds d'un réseau, on ajoute une nouvelle branche, celle-ci sera parcourue par le même courant que si on remplaçait le réseau par un générateur de tension :

  • dont la f.é.m serait égale à la tension à vide entre les deux nœuds

  • dont la résistance interne serait la résistance du réseau "vu de ces points"

Remarque

Pour calculer la résistance interne du générateur, on ne conserve que les éléments passifs[2] du réseau: chaque générateur est remplacé par sa résistance interne.

ExempleExemple

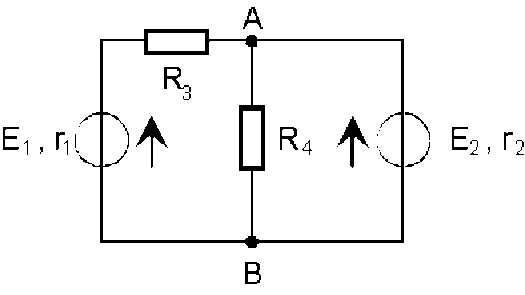
Dans le réseau ci-dessus, pour calculer l' intensité[3] du courant traversant l'élément de résistance \(R_4\), on peut procéder en deux étapes :

  • calculer les caractéristiques du générateur de tension équivalent au réseau (dans lequel on a enlevé la branche contenant l'élément de résistance \(R_4\) )"vu de \(A \textrm{ et }B\)"

  • remplacer le réseau par le générateur pour calculer le courant traversant l'élément de résistance \(R_4\)

Première étape :

  • calcul de la tension à vide :

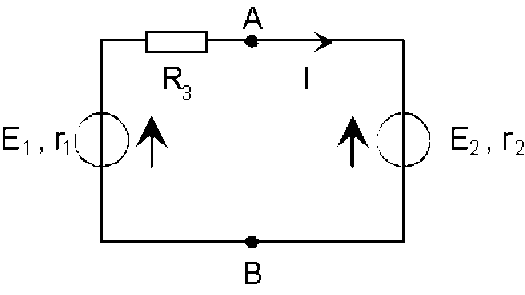
comme on ignore les valeurs des forces électromotrices, il est impossible de prévoir le sens du courant dans le circuit; on choisit un sens arbitraire; avec le sens choisi sur le schéma ci-dessus, l'intensité du courant a pour valeur :

\(\displaystyle{I=\frac{E_1-E_2}{r_1+r_2+R_3}}\)

(si la valeur numérique obtenue par la suite est négative, c'est que le courant circule dans l'autre sens) l'application de la loi d'Ohm nous donne :

\(\displaystyle{V_A-V_B=E_1-(r_1+R_3).I=E_2+r_2.I=\frac{(r_1+R_3).E_2+r_2.E_1}{r_1+r_2+R_3}}\)

  • calcul de la résistance du réseau vu de A et B :

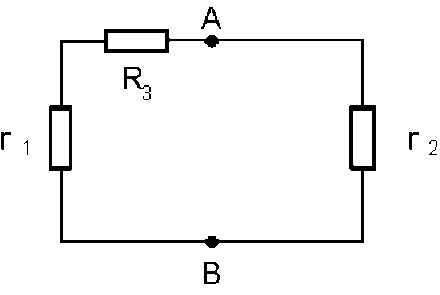
on remplace les générateurs par leur résistance interne. Vu des noeuds A et B, le réseau est formé de deux branches en parallèle, d'où sa résistance :

\(\displaystyle{R_{AB}=\frac{(r_1+R_3).r_2}{r_1+r_2+R_3}}\)

Deuxième étape :

  • calcul du courant traversant l'élément de résistance \(R_4\).

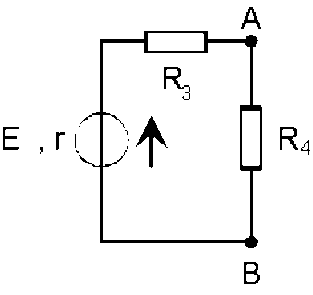
On remplace le réseau par un générateur de tension de f.é.m. \(E = V_A-V_B\) et de résistance interne \(r = R_{AB}\) ; d'où l'intensité du courant :

\(\displaystyle{I_4=\frac{E}{r+R_4}=\frac{E_1.r_2+E_2.(r_1+R_3)}{r_1r_2+r_1R_4+r_2R_3+r_2R_4+R_3R_4}}\)