Méthode des courants de maille
Une fois qu'on a déterminé m mailles indépendantes (par la méthode du squelette, par exemple), on attribue à chacune un courant de maille de sens arbitraire. On écrit ensuite les équations de maille avec la convention suivante :
Règle :
Quand une branche appartient à plusieurs mailles, le courant dans cette branche est la somme algébrique des ces courants de maille.
Exemple :
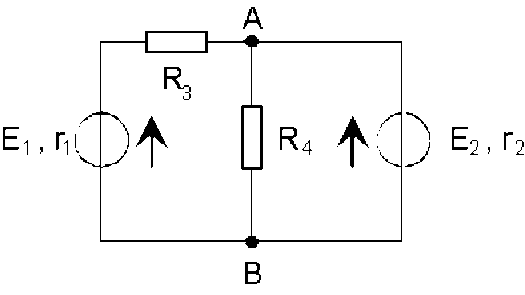
Dans le réseau ci-dessus, pour calculer l' intensité[1] du courant traversant l'élément de résistance[2] \(R_4\), on peut procéder comme suit :
on cherche un squelette du circuit ; comme il n'y a que deux noeuds, chacune des branches peut être prise comme squelette; puisqu'on cherche l'intensité dans \(R_4\), il y a intérêt à ce que ce soit une des inconnues du système ; il faut donc prendre comme squelette une des autres branches, par exemple celle de gauche.
en ajoutant la branche centrale au squelette, on obtient une première maille indépendante, parcourue par un courant de maille d'intensité \(I_4\), dans le sens des aiguilles d'une montre.
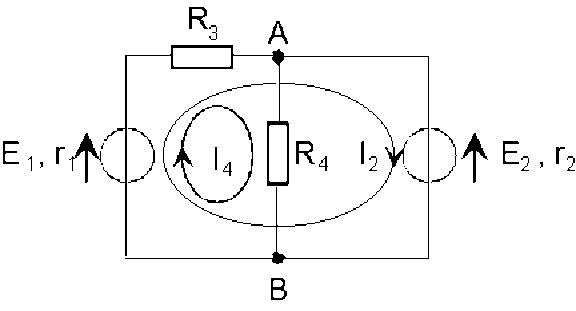
en ajoutant la branche de droite au squelette, on obtient une deuxième maille indépendante, parcourue par un courant de maille d'intensité \(I_2\), dans le sens des aiguilles d'une montre.
le squelette appartient aux deux mailles : il est donc parcouru par les deux courants de maille ; avec la convention de sens choisie, les intensités s'ajoutent.
il faut maintenant écrire les équations de maille :
Première maille :
\(\displaystyle{{E}_{{1}}-{\left({r}_{{1}}+{R}_{{3}}\right)}.{\left({I}_{{2}}+{I}_{{4}}\right)}-{R}_{{4}}.{I}_{{4}}={0}}\)
Deuxième maille :
\(\displaystyle{{E}_{{1}}-{\left({r}_{{1}}+{R}_{{3}}\right)}.{\left({I}_{{2}}+{I}_{{4}}\right)}-{r}_{{2}}.{I}_{{2}}-{E}_{{2}}={0}}\)
qui conduisent à un système de deux équations à deux inconnues :
\(\displaystyle{{\left({r}_{{1}}+{R}_{{3}}\right)}.{I}_{{2}}+{\left({r}_{{1}}+{R}_{{3}}+{R}_{{4}}\right)}.{I}_{{4}}={E}_{{1}}}\)
\(\displaystyle{{\left({r}_{{1}}+{r}_{{2}}+{R}_{{3}}\right)}.{I}_{{2}}+{\left({r}_{{1}}+{R}_{{3}}\right)}.{I}_{{4}}={E}_{{1}}-{E}_{{2}}}\)
ayant pour solution :
\(\displaystyle{{I}_{{4}}=\frac{{{E}_{{1}}.{r}_{{2}}+{E}_{{2}}.{\left({r}_{{1}}+{R}_{{3}}\right)}}}{{{r}_{{1}}{r}_{{2}}+{r}_{{1}}{R}_{{4}}+{r}_{{2}}{R}_{{3}}+{r}_{{2}}{R}_{{4}}+{r}_{{3}}{R}_{{4}}}}}\)