Application
Durée : 2 mn
Note maximale : 6
Question
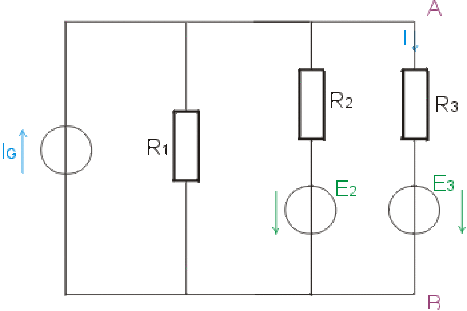
On considère le réseau électrique ci-dessous. On veut calculer l'intensité \(I\) dans la branche \(3\) par application du théorème de superposition.
a- On appellera \(I_1,\) \(I_2,\) \(I_3\) les intensités des courants dans la branche \(3,\) correspondant respectivement aux régimes \(E_2\) et \(E_3\) éteintes, \(I_G\) et \(E_2\), éteintes, \(I_G\) et \(E_3\) éteintes.
Faire les schémas de ces \(3\) régimes et écrire sous chaque schéma la relation liant (\(V_A-V_B\)) au courant.
b- Simplifier chacun de ces schémas et en déduire \(I_1,\) \(I_2,\) \(I_3\) et \(I\).
Solution
1 : Calcul du courant \(I\) créé par le générateur de courant dans \(R_3\) :
Le schéma du montage est :
C'est un diviseur de courant, donc : \(\displaystyle{ I_1 = I_G . \frac{G_3}{G_1 +G_2 + G_3} }\) où \(G_1\), \(G_2\), \(G_3\) sont les conductances de \(R_1\), \(R_2\), \(R_3\)
\(\displaystyle{ I_1 = 1 . \frac{\frac{3}{2}}{\frac{1}{2} + \frac{1}{4} + \frac{3}{2}} = \frac{2}{3} \mathrm{ A} }\) , de \(A\) vers \(B\)
\(\displaystyle{ V_A - V_B = R_3 . I_1 = \frac{I_G}{G_1 + G_2 + G_3} = \frac{4}{9} \mathrm{ V} }\) (1 pt)
2 : Calcul du courant \(I_2\) créé par le générateur de tension \(E_3\) dans \(R_3\) :
Le schéma du montage est :
Soit \(R_{12}\) la résistance équivalente à l'ensemble \(R_1\), \(R_2\).
En remplaçant \(R_{12}\) par son expression : \(\displaystyle{ R_{12} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} } = \frac{1}{\frac{1}{2} + \frac{1}{4} } = \frac{4}{3} \mathrm{ } \Omega }\)
\(\displaystyle{ I_2 = 1 . \frac{\frac{1}{3}}{\frac{2}{3} + \frac{4}{3}} = \frac{1}{6} \mathrm{ A} }\), de \(A\) vers \(B\)
\(\displaystyle{ V_A-V_B = R_3 . I_2 - E_3 = - R_{12} . I_2 = -\frac{2}{9} \mathrm{ V} }\) (1 pt)
3 : Calcul du courant \(I_3\) créé par le générateur de tension \(E_2\) dans \(R_3\) :
Le schéma du montage est :
Soit \(I\) l'intensité du courant débité par le générateur, et \(R_{13}\) la résistance équivalente à l'ensemble \(R_1\), \(R_3\).
\(\displaystyle{ I = \frac{E_2}{R_2 + R_{13}}}\)
\(\displaystyle{ R_{13} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_3} } = \frac{1}{\frac{1}{2} + \frac{3}{2} } = \frac{1}{2} \mathrm{ } \Omega }\)
\(\displaystyle{ I = \frac{E_2}{R_2 + R_{13} } = \frac{8}{2 + \frac{1}{2}} = \frac{16}{3} \mathrm{ A} }\)
L'ensemble \(R_1\), \(R_3\) est un diviseur de courant :
\(\displaystyle{ I_3 = I . \frac{G_3}{G_1 + G_3} = I . \frac{R_1}{R_1 + R_3} = \frac{16}{3} . \frac{2}{2 + \frac{2}{3} } = 4 \mathrm{ A}}\), de \(B\) vers \(A\)
\(\displaystyle{ V_A-V_B = - R_3 . I_3 = R_2 . I - E_2 = - \frac{8}{3} \mathrm{ V} }\) (1 pt)
Quand les \(3\) générateurs débitent, le courant dans \(R_3\) a pour valeur : \(I_T = \overline{I_1} + \overline{I_2} + \overline{I_3}\) (valeurs algébriques)
\(\displaystyle{ I_T = - \frac{2}{3} - \frac{1}{6} + 4 = \frac{11}{6} \mathrm{ A} }\), de \(B\) vers \(A\)


