Q égales aux sommets d'un triangle
Durée : 5 mn
Note maximale : 10
Question
Trois charges \(q, q\) et \(2q\) sont situées aux sommets d'un triangle équilatéral de coté \(a\).
En vous aidant du théorème de superposition, exprimer le champ \(\vec E\) existant au centre de gravité du triangle.
Solution
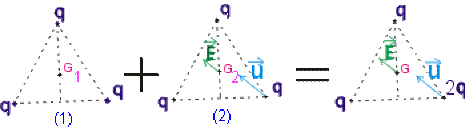
\(\vec E_{G_1}=\vec0\)
\(\vec E_{G_2}=\frac q{4\pi\epsilon_0d^2}\vec u\)
\(\vec E_G=\vec E_{G_1}+\vec E_{G_2}=\frac q{4\pi\epsilon_0d^2}\vec u\)
\(d=\frac{2}3\cdot\frac{a\sqrt3}2=\frac{a\sqrt3}3\Rightarrow E_G=\frac{3q}{4\pi\epsilon_0a^2}\)
Évaluation :
Séparation des deux situations : 5 pts
Expression de \(E_G\) : 5 pts