Théorème de Gauss et symétrie cylindrique
Durée : 8 mn
Note maximale : 30
Question
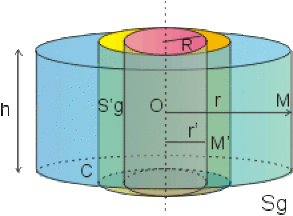
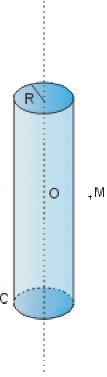
Un cylindre métallique \(C\) de rayon \(R\) et de hauteur \(h\) très grande devant la distance d'observation porte une charge \(Q\) uniformément répartie sur sa surface latérale.
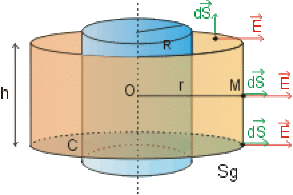
Quelle surface de Gauss \(Sg\) faut-il choisir pour déterminer \(\vec E\) en un point \(M\) grâce au théorème de Gauss (\(OM\) supposé \(<<h\)).
Exprimer le flux\(\Phi\) de \(\vec E\) à travers \(Sg\) en fonction de \(E\) et de \(r\).
Déterminer le champ \(\vec E\) créé en un point \(M\) extérieur ou extérieur au cylindre \(C\).
Solution
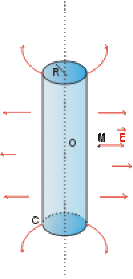
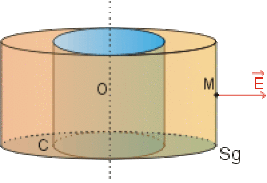
1. Loin des extrémité du cylindre les lignes de champ \(\vec E\) sont radiales. La surface fermée \(Sg\) passant par \(M\) et possédant les propriétés de symétrie de la source est celle d'un cylindre \(Sg\) de rayon \(r\) (\(r\) est la variable d'espace définissant la position du point \(M\)) (10pts)
_________________________________________________________________________________________________________________________________________________________________________
2. En tout point des sections droites de \(Sg\), \(\vec E\) est orthogonal à \(d\vec S\).
D'où \(\vec E.d\vec S=0~\Phi=0\) à travers les sections droites.
En tout point de la surface latérale du cylindre \(Sg\), \(\vec E\) est colinéaire à \(d\vec S\) et \(E\) prend la même valeur par symétrie. \(E\) peut donc être sortie de de l'intégrale :
\(\Phi= \displaystyle{\iint_{S_\textrm{lat\'erale}}\vec E.d\vec S = \iint_{S_\textrm{lat\'erale}}E.dS=E \iint_{S_\textrm{lat\'erale}}\vec E.d\vec S}\)
\(\Phi=E.2.\pi.r.h\) 10 pts
_________________________________________________________________________________________________________________________________________________________________________
3. \(\Phi=\displaystyle{\iint_{S_g}\vec E.\vec{dS}=E2\pi.r.h}\)
D'autre part \(\Phi=\frac{Q_\textrm{int}}{\epsilon_0}\) (théorème de Gauss)
A l'extérieur du cylindre \(C\), la charge \(Q_\textrm{int}\) intérieure à \(S_g\) est \(Q_\textrm{int}=Q\)
\(\Phi=E.2.\pi.r.h=\frac{Q}{\epsilon_0}E_\textrm{ext}=\frac{Q}{2\pi\epsilon_0 rh}\)
en appelant \(\lambda=\frac{Q}{h}\quad\Rightarrow\quad E_\textrm{ext}=\frac{\lambda}{2\pi\epsilon_0 r}\)
*A l'intérieur du cylindre \(C\), il n'y a pas de charge
\(\Phi=E.2\pi.r.h=0\)
\(E_\textrm{int}=0\) 10 pts