Symétrie sphérique 1/1
Partie
Question
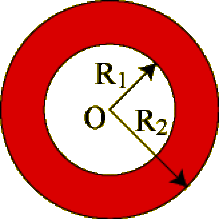
Le volume compris entre les surfaces définies par deux sphères concentriques de centre \(O\) et de rayons respectifs \(R_1\) et \(R_2\) (\(R_1< R_2\)) est chargé uniformément par une densité volumique de charges constante (\(\rho > 0\)). Le reste de l'espace (intérieur de la sphère de rayon \(R_1\) et de volume extérieur à la sphère de rayon \(R_2\)) ne comporte aucune charge.
Calculer à l'aide du Théorème de Gauss le champ électrique \(\vec E\) à la distance \(r\) du centre. Distinguer les 3 cas : \(r< R_1\) , \(r > R_2\) , \(R_1 < r < R_2\) .
Y a-t-il continuité du champ aux interfaces \(r = R_1\) et \(r = R_2\) ?
Aide simple
La surface de Gauss est une sphère de centre \(O\) et de rayon \(r\). Remarquez que les vecteurs \(\vec E\) (champ radial) et \(\mathrm d \vec S\) sont colinéaires, de même sens (\(\rho > 0\)) et que l'amplitude de \(E\) est constante en tout point de la surface de Gauss.
Aide détaillée
Le flux à travers la sphère de Gauss s'écrit :
\(\oiint_S \vec E . \mathrm d \vec S = \oiint_S E . \mathrm d S = E \oiint_S \mathrm d S = E ~ S = E ~ 4 \pi r^2\)
Solution simple
\(r > R_2~~\) \(~~E = \frac{\rho \big( R_2^3 - R_1^3 \big)}{3 \epsilon_0 ~ R_2^2}\)
\(R_1 < r < R_2~~\) \(~~E = \frac {\rho\big( r^3 - R_1^3\big)}{3 \epsilon_0 ~ r^2}\)
\(r < R_1~~\) \(~~E = 0\).
Solution détaillée
Le volume est à symétrie sphérique : la surface de Gauss \(S\) choisie sera donc une sphère de centre \(O\) et de rayon \(r\), \(r\) pouvant prendre 3 valeurs : \(r < R_1\) ou \(R_1< r < R_2\) ou \(r >R_2\) .
Remarquons que :
- \(\vec E\) est radial et \(||\vec E||\) est identique en tous points de \(S\).
- \(\vec E\) et \(\mathrm d \vec S\) sont colinéaires et de même sens puisque (\(\rho > 0\)).
Calculons le flux à travers \(S\) :
\(\oiint_S \vec E . \mathrm d \vec S = \oiint_S E . \mathrm d S = E \oiint_S \mathrm d S = E ~ S = E ~ 4 \pi r^2\)
Appliquons le théorème de Gauss dans les 3 cas.
PREMIER CAS : \(r > R_2\)
La charge à l'intérieur de la sphère de Gauss est comprise entre les 2 sphères de rayon \(R_1\) et \(R_2\) donc le volume contenant la charge est
\(V = \frac{4}{3} \pi R_2^3 ~ - ~ \frac{4}{3} \pi R_1^3\).
Appliquons le théorème de Gauss
\(E ~ 4 \pi r^2 = \frac{\rho \frac{4}{3} \pi \big( R_2^3 - R_1^3\big)}{\epsilon_0}\)
\(E = \frac{\rho \big( R_2^3 - R_1^3\big)}{3 ~ \epsilon_0 ~ r^2}\)
DEUXIEME CAS : \(R_1< r <R_2\)
La charge à l'intérieur de la sphère de Gauss est comprise entre les 2 sphères de rayon \(r\) et \(R_1\) donc le volume contenant la charge est
\(V = \frac{4}{3} \pi r^3 ~ - ~ \frac{4}{3} \pi R_1^3\).
Appliquons le théorème de Gauss
\(E ~ 4 \pi r^2 = \frac{\rho \frac{4}{3} \pi \big( r^3 - R_1^3\big)}{\epsilon_0}\)
\(E = \frac{\rho \big( r^3 - R_1^3\big)}{3 ~ \epsilon_0 ~ r^2}\)
TROISIEME CAS : \(r < R_1\)
La charge à l'intérieur de la sphère de Gauss est nulle puisque la charge est nulle dans la sphère de rayon \(R_1\) donc le champ est nul à l'intérieur de la sphère de rayon \(R_1\).
CONTINUITE DU CHAMP
si \(r = R_1^-~~\), \(~~E = 0\)
si \(r = R_1^+~~\), \(~~E = \frac{\rho \big( r^3 - R_1^3\big)}{3 ~ \epsilon_0 ~ r^2}~\) avec \(r = R_1\)
donc \(E\) est nul.
Il y a bien continuité du champ à l'interface \(R_1\).
si \(r = R_2^-~~\), \(~~E = \frac{\rho \big( r^3 - R_1^3\big)}{3 ~ \epsilon_0 ~ r^2}~\) avec \(r = R_2\).
si \(r = R_2^+~~\), \(~~E = \frac{\rho \big( R_2^3 - R_1^3\big)}{3 ~ \epsilon_0 ~ R_2^2}~\)
Il y a égalité des champs de part et d'autre de l'interface, le champ est donc continu à l'interface \(R_2\).