Théorème d'Ampère appliqué à un solénoïde (2)
Partie
Question
Soit un solénoïde parcouru par un courant d'intensité \(I\), constitué de \(n\) spires par unité de longueur.
Soit un contour fermé orienté \(\mathcal{C}\) dont la dimension le long de l'axe \(z\) est \(d\), comme indiqué sur la figure.
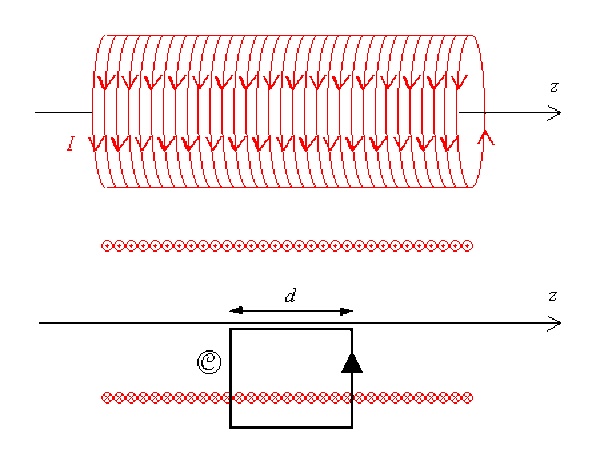
Exprimer la circulation du champ magnétostatique \(\vec B\) le long du contour \(\mathcal{C}\), en fonction de \(I\), \(d\) et \(n\).
Aide simple
La circulation de \(\vec B\) le long d'un contour fermé \(\mathcal{C}\) est donnée par le théorème d'Ampère.
Rappel de cours
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
D'après le théorème d'Ampère, la circulation de \(\vec B\) le long d'un contour fermé \(\mathcal{C}\) s'écrit :
\(\displaystyle{ \oint_{\mathcal{C}} \vec B . \vec{\mathrm{d}l} = \mu_0 . \sum I }\)
où le terme \(\displaystyle{ \sum I}\) fait la somme algébrique des courants qui traversent \(\mathcal{C}\).
Ici plusieurs spires traversent \(\mathcal{C}\).
Leur nombre \(N\) dépend de la dimension \(d\) du contour : \(N = n . d\)
L'application de la règle du tire-bouchon au contour orienté \(\mathcal{C}\) permet de déterminer le sens de la normale à \(\mathcal{C}\) :
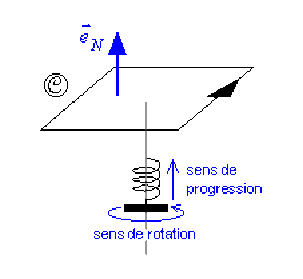
Or le courant dans les spires qui traversent \(\mathcal{C}\) fuit vers l'arrière de la figure, il sera donc compté négativement.
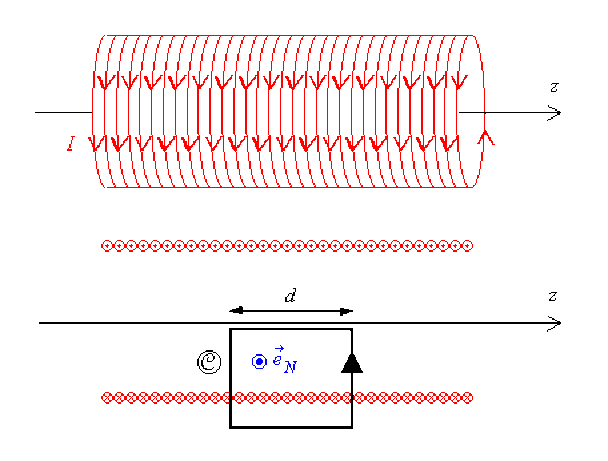
En conclusion : \(\displaystyle{ \oint_{\mathcal{C}} \vec B . \vec{\mathrm{d}l} = - \mu_0 . N . I = - \mu_0 . n . d . I }\)