Champ de Hall - D. D. P. de Hall
Considérons un conducteur métallique de section rectangulaire de côtés \(\mathsf{a}\) et \(\mathsf{b}\), parcouru par un courant continu d'intensité \(\mathsf{I}\) ; il y a \(\mathsf{n}\) électrons de conduction, de charge \(e = -1,6 . 10^{-19}\mathrm{C}\), par unité de volume qui se déplacent à la vitesse \(\vec v\).
Le courant étant continu et le conducteur de section constante, on a :
\(I = J .ab\) avec \(\vec J = \rho_m \vec v = n e \vec v\)
Les lignes de courant sont rectilignes.
Plaçons ce barreau dans un champ magnétique extérieur \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\)
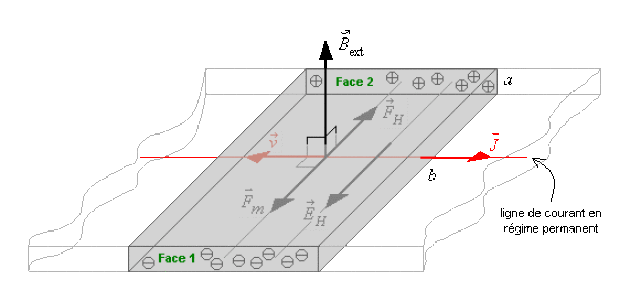
Les électrons de conduction sont soumis à la force de Laplace \(\vec F_m = e \vec v \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\) qui infléchit leur trajectoire vers la face 1 (voir schéma) où se produit une accumulation d'électrons.
Alors par influence, des charges positives apparaissent sur la face 2 (voir schéma).
Un champ électrique \(\vec E_H\), appelé champ de Hall, apparaît ainsi dans le conducteur et il croît au cours de ce régime transitoire au fur et à mesure que les charges s'accumulent.
Ce champ va exercer sur les électrons de conduction une force \(\vec F_H = e \vec E_H\), opposée à la force \(\vec F_m\).
Au cours de cette accumulation et au bout d'un certain temps, lorsque \(\vec E_H\) sera suffisamment grand pour que \(\vec F_m = - \vec F_H\), alors :
\(\vec F_m + \vec F_H = [e \vec E_H] + [e \vec v \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}] = \vec 0\).
Les électrons de conduction ne seront plus déviés.
Donc : \(\vec E_H = - \vec v \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\) ce qui donne \(E_H = v B_{\mathrm{ext}}\).
Les lignes de courant redeviennent rectilignes, l'accumulation des charges cesse et on retrouve le régime permanent.
Ce champ de Hall crée une différence de potentiel entre les faces 1 et 2 (voir schéma) ; cette d.d.p. de Hall s'écrit :
\(V_2 - V_1 = E_H . b = v B_{\mathrm{ext}} b = \frac{J}{n|e|} b B_{\mathrm{ext}} = \frac{I}{n|e|a}B_{\mathrm{ext}}\)