Cadre rectangulaire dans un champ extérieur
Durée : 8 mn
Note maximale : 5
Question
Un cadre rectangulaire suspendu par un fil de torsion est placé dans un champ magnétique extérieur \(\vec{B_{ext}}\) parallèle à ses côtés horizontaux. Lorsqu'il est parcouru par un courant continu d'intensité 0,8 A, il tourne d'un angle \(\theta_1 = 30°\).
Quelle est l'intensité du courant continu qui le traverse quand il tourne de 45° ?
Solution
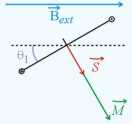
Le cadre est soumis au moment du couple magnétique et au moment du couple de rappel du fil de torsion.
A l'équilibre, on a : \(C.\theta_1=\mathcal M_1B_{ext}\sin\left(\frac{\pi}{2}-\theta_1\right)\) avec \(\mathcal M_1=nI_1S\)
Lors du second équilibre, on a : \(C.\theta_2=\mathcal M_2B_{ext}\sin\left(\frac{\pi}{2}-\theta_2\right)\) avec \(\mathcal M_2=nI_2S\)
On a donc : \(C\theta_1=nI_1SB_{ext}\cos\theta_1\) et
\(C\theta_2=nI_2SB_{ext}\cos\theta_2\)
soit \(\frac{\theta_1}{\theta_2}=\frac{I_1}{I_2}\frac{\cos\theta_1}{\cos\theta_2}\)
Ainsi \(I_2=I_1\frac{\cos\theta_1}{\cos\theta_2}\frac{\theta_2}{\theta_1}\)
soit \(I_2=\textrm{0,8}\frac{\cos30°}{\cos45°}\frac{\frac{\pi}{4}}{\frac{\pi}{6}}=\textrm{1,47 }A\)
5 pts