Plus courte traversée entre deux ports
Durée : 8 mn
Note maximale : 8
Question
Sur la sphère terrestre de rayon \(R\), deux ports \(A\) et \(B\) de l'Océan Pacifique sont repérés par leurs coordonnées angulaires \(\theta_A, \varphi_A\) et \(\theta_B, \varphi_B\).
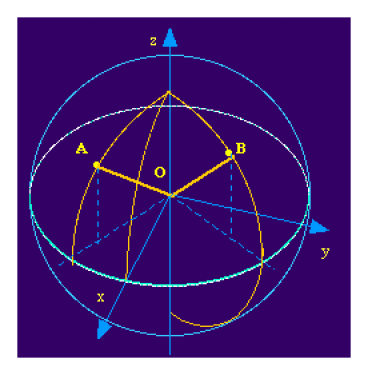
Quelle est la distance minimale que peut parcourir un bateau pour relier \(A\) à \(B\) ?
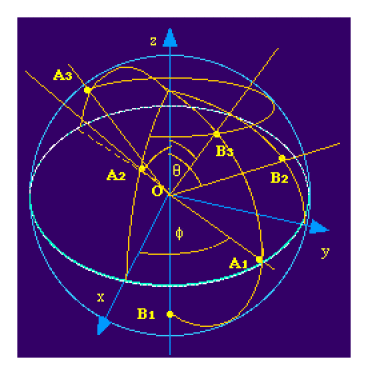
Calculez cette distance en fonction de \(R\) dans les cas particuliers suivants ( où \(A\) et \(B\) ne désignent plus nécessairement des ports ) :
1. \(\displaystyle{\theta_A=\frac{\pi}{2}}\quad\varphi_A=\varphi\quad\theta_B=\pi\quad\varphi_B=\varphi\)
2. \(\displaystyle{\theta_A=\theta\quad\varphi_A=0\quad\theta_B=\varphi\quad\varphi_B=\frac{\pi}{2}}\)
3. \(\displaystyle{\theta_A=\frac{\pi}{3}\quad\varphi_A=\varphi-\pi\quad\theta_B=\frac{\pi}{6}\quad\varphi_B=\phi}\)
Vérifiez que les résultats obtenus sont conformes à ceux que prévoit la géométrie.
Solution
La distance la plus courte est la longueur de l'arc AB : \(AB = R(\vec{OA},\vec{OB})\).
(1 point)
On a d'autre part, \(\vec{OA}.\vec{OB}=R^2\cos(\vec{OA},\vec{OB})\).
(1 point)
En fonction des coordonnées angulaires on a :
\(\cos(\vec{OA},\vec{OB})=\sin\theta_A\sin\theta_B(\cos\phi_A\cos\varphi_B+\sin\varphi_A\sin\varphi_B)+\cos\theta_A\cos\theta_B\)
(2 points)
ou bien \(\sin\theta_A\sin\theta_B \cos (\varphi_A - \varphi_B) + \cos \theta_A \cos\theta _B\).
(1 point)
1. \(\cos(\vec{OA}.\vec{OB})=\cos(\theta_A-\theta_B)=0\)
\(\displaystyle{AB}=R\textrm{ Arccos }0=R\left(\frac{\pi}{2}\right)\)
(qui peut être obtenu géométriquement).
(1 point)
2)\(\cos(\vec{OA}.\vec{OB})=\cos^2\theta\)
\(AB=R\mathrm{ Arc }\cos(\cos^2\theta)\) si \(\displaystyle{\theta=\left(\frac{\pi}{2}\right)}\), on a \(\displaystyle{AB=R\left(\frac{\pi}{2}\right)}\)
(1 point)
3) \(\cos(\vec{OA}.\vec{OB})=\cos(\theta_A+\theta_B)=0\)
\(\displaystyle{AB=R \mathrm{ Arc }\cos0=R\left(\frac{\pi}{2}\right)}\)
(qui peut être obtenu géométriquement).
(1 point)