Pythagore : généralisation
Durée : 7 mn
Note maximale : 7
Question
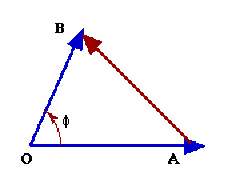
Deux points matériels sont repérés par les vecteurs \(\vec{OA}\) et\( \vec{OB}\).
Quelle est la distance qui les sépare ( amplitude du déplacement \(AB\) ) ?
Exprimez cette distance en fonction des normes \(a = OA\) et \(b = OB\) de \(\vec{OA}\) et\( \vec{OB}\) de l'angle \(\varphi=( \vec{OA}. \vec{OB})\).
Vérifiez le résultat obtenu dans le cas où \(\displaystyle{\varphi=\frac{\pi}{2}}\).
Y a-t-il d'autres valeurs remarquables de \(\varphi\) permettant de contrôler le résultat ?
Peut-on faire d'autres contrôles en jouant sur les valeurs de \(a\) et \(b\)?
Solution
On a \(\vec{AB}=\vec{OB}-\vec{OA}\) et \(\vec{AB^2}=\vec{OA^2}+\vec{OB^2}-2\vec{OA}.\vec{OB}\),
(1 point)
et donc \(AB=\sqrt{(a^2+b^2+2ab\cos\varphi)}\)
(1 point)
Lorsque \(\displaystyle{\varphi=\frac{\pi}{2}}\), on retrouve le théorème de Pythagore :
\(AB=\sqrt{a^2+b^2}\).
(1 point)
Lorsque \(\varphi = 0\) ou \(\pi\), \(AB\) est la différence ou la somme de \(a\) et \(b\).
On vérifie qu'on a bien : \(AB=\sqrt{(a^2+b^2+2ab \cos\varphi)}=|a-b| \mathrm{ ou }a+b\).
(2 points)
Enfin, si on pose \(b = a\), le triangle \(AOB\) est isocèle : si de plus \(\displaystyle{\varphi=\frac{\pi}{3}}\), il est équilatéral et \(AB=a\).
On vérifie qu'on a bien \(AB=\sqrt{ 2a^2-2a^2\left(\frac{1}{2}\right)}=a\)
(2 points)