Produit scalaire
Durée : 3 mn
Note maximale : 3
Question
On impose au produit scalaire de deux vecteurs \(\vec{OA}\) et \(\vec{OB}\) et de normes \(OA\) et \(OB\):
- d'être nul, lorsque \(\vec{OA}\) et \(\vec{OB}\) sont portés par deux droites perpendiculaires.
- d'être égal au produit \(OA.OB\) de leurs normes, lorsqu'ils sont portés par une même droite.
On représente le produit scalaire par la forme \(\vec{OA}.\vec{OB}=\vec{OB}.\vec{OA}\)
Montrez que ces conditions permettent de faire un choix entre les deux expressions \(\vec{OA}.\vec{OB}=C\sin\varphi\) et \(\vec{OA}.\vec{OB}=C\cos\varphi\)
où \(\varphi\) est l'angle formé par les deux droites orientées qui portent \(\vec{OA}\) et \(\vec{OB}\) et où \(C\) est une constante réelle positive.
En déduire l'expression de la constante \(C\).
Solution
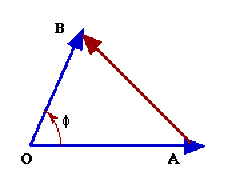
C'est évidemment l'expression \(\vec{OA}.\vec{OB}=C\cos\varphi\) qui convient puisqu'elle seule est nulle lorsque :
\(\displaystyle{\varphi=\frac{\pi}{2}}\) et qu'elle est une fonction paire de la variable \(\varphi\).
(2 points)
Dans le cas où \(\varphi = 0\), la seconde condition impose que \(C = OA OB\).
Finalement, \(\vec{OA}.\vec{OB}=OA OB\cos\varphi\)
(1 point)