Déplacement dû à la variation d'une coordonnée (en cylindrique)
Durée : 3 mn
Note maximale : 3
Question
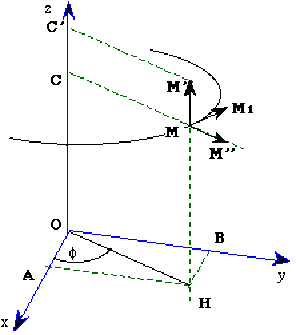
Le vecteur \(\vec{OM}\) détermine la position d'un point \(M\) de l'espace par rapport à un repère rectangulaire direct \((O: x, y, z)\).
Le vecteur \(\vec{MM'}\) détermine le déplacement d'un mobile ponctuel entre les points \(M\) et \(M'\).
Exprimez en coordonnées cylindriques \((\rho, \varphi, z)\), la mesure algébrique ds de chaque élément de courbe décrit par \(M\) lorsqu'on donne un accroissement infinitésimal à l'une des coordonnées, les autres restant constantes.
Solution
Lorsque \(\rho\) et \(\varphi\) sont fixés, l'accroissement \(dz\) de \(z\) correspond à un segment \(MM'\) sur une droite parallèle à \(Oz\).
On a \(\overline{MM'}=\overline{CC'}\) soit \(ds=dz\).
(1 point)
Lorsqu'on fixe \(z\) et \(\theta\), \(MM''\) est un segment de la demi-droite \([CM)\).
On a \(ds=\overline{MM''}=dr\).
(1 point)
Lorsque \(\rho\) et \(z\) sont fixés, \(MM_1\) est un arc du cercle de centre \(C\) et de rayon \(r\). On a \(ds=MM_1=rd\varphi\)
(Pour un déplacement infinitésimal, les arcs de courbe sont assimilables à des segments de droite : on a \(MN\simeq\overline{MN}\))