Chemin hélicoïdal
Durée : 8 mn
Note maximale : 8
Question
Dans un référentiel d'espace-temps à trois dimensions, les événements sont repérés par les coordonnées polaires \((r, \varphi)\) dans le plan \(xOy\), et \(t\) sur l'axe du temps : \(E(r, \varphi, t)\).
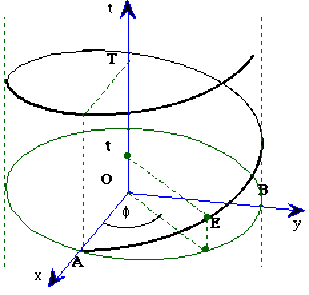
Dans ce référentiel, le mouvement d'un point matériel est décrit par un chemin hélicoïdal tel que :
\(r = R\), \(\displaystyle{\varphi=\frac{2\pi t}{T}}\)
Décrivez le mouvement aussi complètement que possible.
Solution
La projection du chemin sur \(xOy\) est la trajectoire : c'est un cercle de centre \(O\) et de rayon \(R\).
(1 point)
Le point matériel est au point \(A\) à l'instant \(t=0\) et à l'instant \(t=T\).
(1 point)
Sa vitesse moyenne entre ces deux instants est égale à \(2\pi R/T\)
(1 point)
A chaque instant, la vitesse
\(\displaystyle{\left|\frac{d\vec{OM}}{dt}\right|=R\frac{d\varphi}{dt}=\frac{2\pi R}{T}}\)
est égal à la vitesse moyenne.
(1 point)
Le mouvement est donc circulaire et uniforme dans le plan.
(1 point)
Les coordonnées du point matériel à chaque instant sont :
\(x(t)=R\cos\frac{2\pi R}{T}\) et \(y(t)=R\sin\frac{2\pi R}{T}\)
Le mouvement est périodique et sa période est \(T\).

(3 points)