Construction de l'ellipse à partir des foyers
Durée : 8 mn
Note maximale : 8
Question
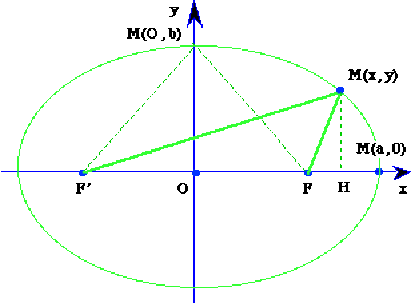
On peut définir l'ellipse comme une courbe plane dont la somme des distances \(MF\) et \(MF'\) de chaque point \(M\) à deux points fixes \(F\) et \(F'\) est constante. Les points \(F\) et \(F'\) sont appelés foyers.
On place le système d'axes orthogonaux \(xOy\) dans le plan de l'ellipse. On choisit d'orienter l'axe \(Ox\) suivant \(F'F\), \(O\) étant au milieu de \(F'F\). On pose
\(MF+MF'=C>0\) et \(OF=-OF'=c\quad \left(0\le c\le\frac{C}{2}\right)\)
Calculez les demi-longueurs \(a\) et \(b\) du grand axe et du petit axe de l'ellipse. Calculez la différence \(MF^2-MF'^2\) et exprimez \(MF\) et \(MF'\) en fonction de \(a\), \(c\) et de l'abscisse \(x\) de \(M\).
Solution
Si \(M\) est sur \(Ox\), \(MF + MF' = MO - OF + MO + OF' = 2MO = 2a\), donc \(a=c/2\).
(1 point)
Si \(M\) est sur \(Oy\), \(MF+MF' = 2MF=2(OF + OM)^{\frac12}\), donc \(b = (a^2 -c^2)^{\frac12}\).
(2 points)
On a
\(MF'^2-MF^2=2a(MF'-MF)\)
ou bien
\(MF'^2-MF^2=(MH^2-HF'^2)-(MH^2+HF^2)=HF'^2-HF^2\)
ainsi
\(\displaystyle{MF'-MF =\frac{(HF'^2-HF'^2)}{2a}=\frac{2OH(F'F)}{2a}=\frac{2cx}{a}}\)
(3 points)
On en déduit :
\(\displaystyle{MF=a-\frac{cx}{a}}\) et \(\displaystyle{MF'=a-\frac{cx}{a}}\)
(2 points)