Cylindre roulant sur un plan
Durée : 6 mn
Note maximale : 8
Question
Un cylindre de rayon \(R\) roule sans glisser sur un plan horizontal.
On choisit de décrire la trajectoire par rapport au repère \(( O : x, y, z)\) tel que :
- l'axe \(Oz\) soit parallèle à l'axe du cylindre,
- le plan \(yOz\) soit le plan horizontal sur lequel roule le cylindre,
- l'axe \(Ox\) soit orienté suivant la verticale ascendante.
On étudie le mouvement d'un point \(M\) de la surface du cylindre dans le plan vertical \(z=0\), sachant qu'il se trouve initialement à l'altitude \(x=2R\).
Établir les équations de la trajectoire de \(M\) en fonction du paramètre angulaire \(\varphi=(Ox,CM)\).
Solution
Il est commode de décomposer le mouvement de la manière suivante :
-une translation du cylindre dans la direction \(Oy\).
-une rotation du cylindre autour de l'axe \(Oz\).
(1 point)
En l'absence de glissement, on a \(\vec{OC}=R\vec{u_x}+R\varphi\vec{u_y}\)
(1 point)
Par rapport au repère \(xCy\) lié à \(C\), on a
\(\vec{CM}=R\cos\varphi\vec{u_x}+R\sin\varphi\vec{u_y}\)
(2 points)
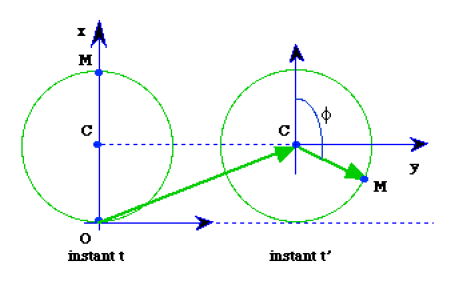
En écrivant que \(\vec{OM}=\vec{OC}+\vec{CM}\) on obtient les équations paramétriques de la trajectoire de \(M\) :
\(x=R(1+\cos\varphi)\), \(y=R(\phi+\sin\varphi)\).
(2 points)