Équation cartésienne de l'ellipse
Durée : 10 mn
Note maximale : 10
Question
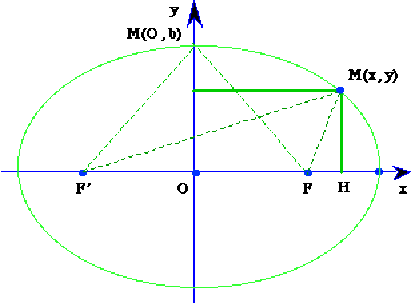
On considère dans le plan \(xOy\), l'ellipse de foyers \(F(c, 0)\) et \(F'( - c, 0)\), avec \(c > 0\),
telle que \(MF'+MF=2a (a > c)\).
Calculez \(MF'^2- MF^2\) puis \(MF'-MF\) et enfin \(MF\) (ou \(MF'\)).
On appelle \(H\) la projection de \(M\) sur l'axe \(Ox\)
Établissez l'équation cartésienne de l'ellipse, en posant \(b^2 = a^2- c^2\).
Solution
On appelle \(H\) la projection de \(M\) sur l'axe \(Ox\). On a alors :
\(\begin{array}{cc}MF'^2-MF^2=(MH^2+HF'^2)-(MH^2+HF^2)=HF'^2-HF^2\\=(x+c)^2-(x-c)^2=4cx\end{array}\)
(3 points)
Mais on peut écrire également :
\(MF'^2-MF^2=(MF'+MF)(MF'-MF)=2a(MF'-MF)\)
On en déduit que
\(MF'-MF=\frac{2cx}{a}\)
(2 points)
Comme \(MF'+MF=2a\), on obtient
\(\displaystyle{MF=a-\frac{cx}{a}}\) ( ou \(\displaystyle{MF=a+\frac{cx}{a}}\))
(1 point)
En élevant \(MF\) au carré, on a
\(MF^2=MH^2+HF^2=y^2+(c-x)^2\) ou bien \(\displaystyle{MF^2=a-\left(\frac{cx}{a}\right)^2}\)
(2 points)
On a, après simplification,
\(\displaystyle{a^2+\left(\frac{cx}{a}\right)^2=c^2+x^2+y^2}\)
puis en ordonnant,
\(\displaystyle{x^2\left(1-\frac{c^2}{a^2}\right)+y^2=a^2-c^2}\)
(1 point)
En posant \(b^2=a^2-c^2\), on obtient finalement,
\(\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}}=1\)
(1 point)